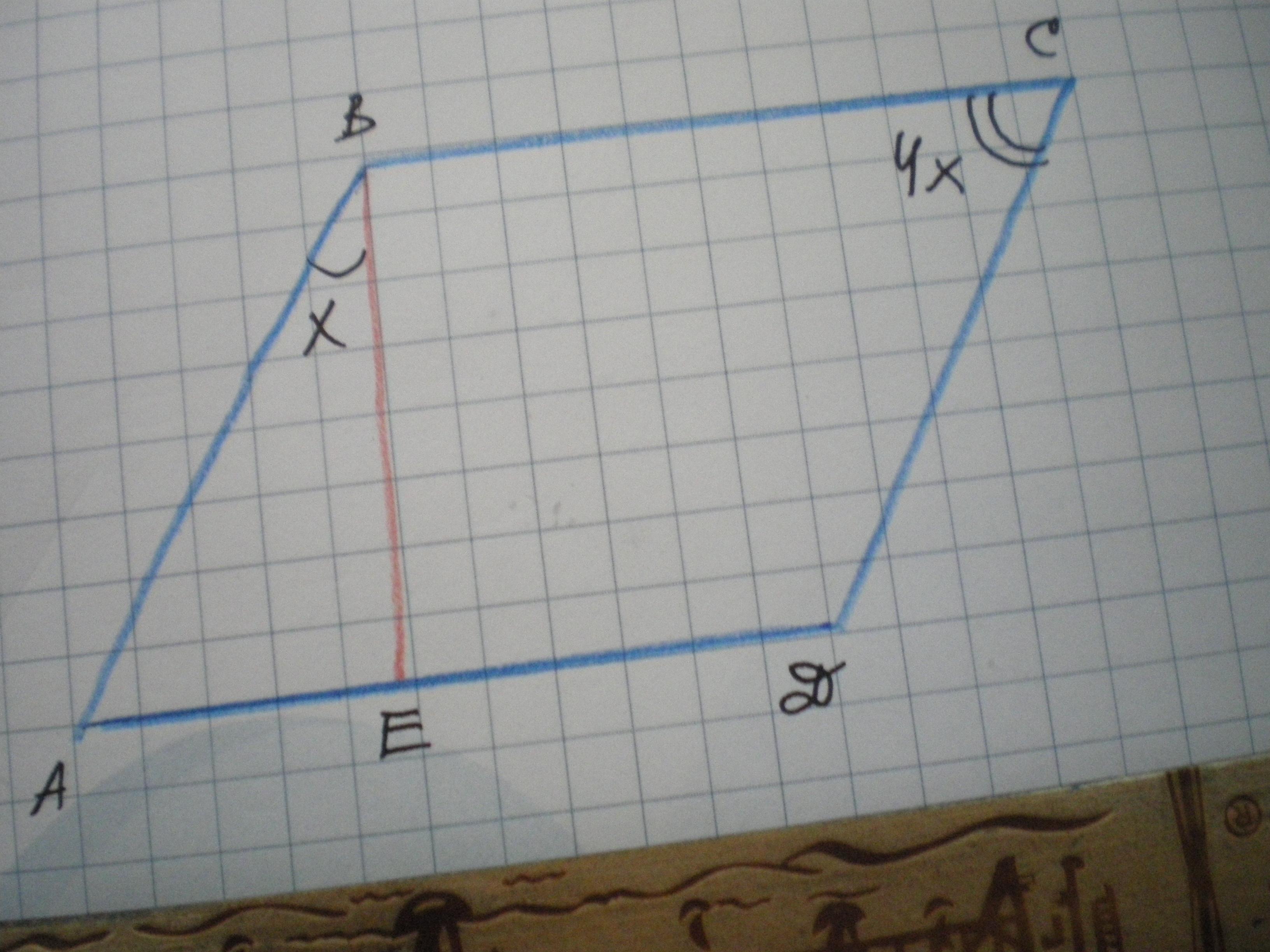
в параллелограме ABCD проведена высота.BE,причем угол BCD в 4 раза больше угла ABE.Найдите угол ABC.

Дано:   параллелограмм ABCD. проведена высота.BE,причем угол BCD в 4 раза больше угла ABE.Найдите угол ABC.Решение:  <BCD=4<ABE=4a

тогда <BAE=90-a  в прямоугольном треугольнике АВЕ

противоположные углы в параллелограмме равны, тогда <BAE=<BCD

90-a = 4a

5a=90

a=18 град 

<ABC=90+a=90+18=108 град

Ответ: <ABC=108 град

Должно быть так, сверь с ответом в учебнике  

Ответ:

108°

Объяснение:

Дано: АВСD - параллелограмм, ВЕ - высота, ∠С=4∠АВЕ. Найти ∠АВС.

Решение: пусть ∠АВЕ=х°, тогда ∠С=∠А=4х° по свойству противоположных углов параллелограмма.

Рассмотрим ΔАВЕ - прямоугольный, сумма острых углов прямоугольного треугольника составляет 90°, поэтому имеем уравнение:

х+4х=90;  5х=90;  х=18.

∠АВЕ=18°,  ∠А=18*4=72°

Сумма углов параллелограмма, прилежащих к одной стороне, составляет 180°, поэтому ∠АВС=180-72=108°.