Предмет: Алгебра, автор: Аноним

помогите молю срочно !!
314-315 упростите выражения
316 докажите тождества :

Приложения:

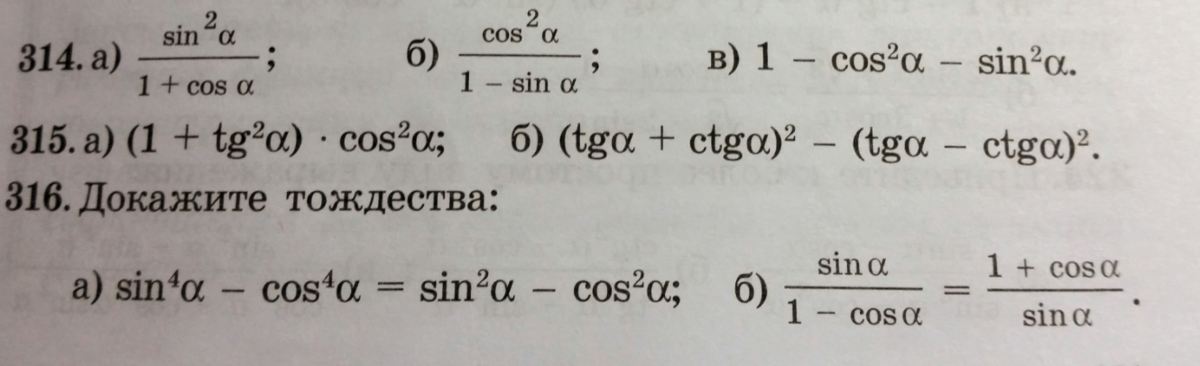
Ответы

Автор ответа: Artem112

$frac{sin^2 alpha }{1+cos alpha } = frac{1-cos^2 alpha }{1+cos alpha } = frac{(1-cos alpha)(1+cos alpha) }{1+cos alpha } =1-cos alpha$
$frac{cos^2 alpha }{1-sin alpha } = frac{1-sin^2 alpha }{1-sin alpha } = frac{(1-sin alpha)(1+sin alpha) }{1-sin alpha } = 1+sin alpha$
$1-cos^2 alpha -sin^2 alpha =1-(cos^2 alpha+sin^2 alpha) =1-1=0$

$(1+tg^2 alpha )cdotcos^2 alpha = frac{1}{ cos^2 alpha }cdot cos^2 alpha =1$
$(tg alpha +ctg alpha )^2-(tg alpha -ctg alpha )^2= \ =tg^2 alpha +2tgalpha ctg alpha+ ctg^2 alpha-(tg^2 alpha -2tgalpha ctg alpha+ ctg^2 alpha)= \ =tg^2 alpha +2tgalpha ctg alpha+ ctg^2 alpha-tg^2 alpha +2tgalpha ctg alpha- ctg^2 alpha= \ =4tgalpha ctg alpha=4cdot1=4$

Учитывая основное тригонометрическое тождество:
$sin^4 alpha -cos^ 4alpha =(sin^2 alpha -cos^ 2alpha )(sin^2 alpha +cos^ 2alpha )= sin^2 alpha -cos^ 2alpha$
Учитывая основное свойство пропорции:
$(1+cos alpha )(1-cos alpha)=1-cos ^2alpha=sin^2 alpha$

Автор ответа: Аноним

а (учитывая основное свойство пропорции:
(1+cos alpha )(1-cos alpha)=1-cos ^2alpha=sin^2 alpha ) это пример под буквой Б да ?

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Математика, автор: zhannametulynska

На 100 кілометрів шляхом мотоцикл витрачаєш 6 л пального. Скільки потрібно пального щоб подолати 400 кілометрів шляху на такому мотоциклі

6 лет назад

Предмет: Математика, автор: pmaksimillifgsfs

математика 6 класс уравнение

6 лет назад

Предмет: Литература, автор: Аноним