Предмет: Алгебра,
автор: elenkaabramova
Докажите неравенство
Приложения:
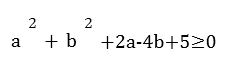
Ответы
Автор ответа:
1
Один из способов доказательства заключается в выделении полных квадратов относительно а и b:
(a^2 + 2a) + (b^2 - 4b) + 5 = (a^2 + 2 * a + 1) - 1 + (b^2 - 2 * 2b + 4) - 4 + 5 = =(a+1)^2 + (b - 2)^2
И теперь нетрудно увидеть, что (a+1)^2 + (b-2)^2 >=0 для любых а и b(как сумма двух квадратов)
(a^2 + 2a) + (b^2 - 4b) + 5 = (a^2 + 2 * a + 1) - 1 + (b^2 - 2 * 2b + 4) - 4 + 5 = =(a+1)^2 + (b - 2)^2
И теперь нетрудно увидеть, что (a+1)^2 + (b-2)^2 >=0 для любых а и b(как сумма двух квадратов)
Интересные вопросы
Предмет: Окружающий мир,
автор: OSTER23232
Предмет: Английский язык,
автор: alenadukareva32
Предмет: Русский язык,
автор: devuchkinan
Предмет: Українська мова,
автор: danyilaOX
Предмет: Математика,
автор: natalya21043