Предмет: Геометрия, автор: gigi12

Прямоугольный треугольник с катетами 3 см. и √3 см., вращается вокруг оси, содержащей его гипотенузу. Найти объем фигуры вращения.

Ответы

Автор ответа: xERISx

ΔABC - прямоугольный - ∠C = 90°; AC = 3 см; BC = √3 см
Теорема Пифагора
AB² = AC² + BC² = 3² + (√3)² = 12
AB = √12 = 2√3 см

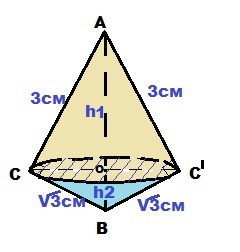
Прямоугольный треугольник вращается вокруг гипотенузы AB. Получилась фигура, состоящая из двух конусов, имеющих общее основание с центром О и радиусом R = CO.
CO - высота прямоугольного треугольника ΔABC - по формуле
$CO= frac{AC*BC}{AB}= frac{3* sqrt{3} }{2 sqrt{3} } =1,5$ см
R = 1,5 см

Объём верхнего конуса $V_1= frac{1}{3} *pi R^2*AO$
Объём нижнего конуса $V_2= frac{1}{3} *pi R^2*BO$
Объём всей фигуры вращения
$V = V_1 + V_2 = frac{1}{3} *pi R^2*AO + frac{1}{3} *pi R^2*BO= \ \ =frac{1}{3} *pi R^2*(AO+BO)=frac{1}{3} *pi R^2*AB= \ \ = frac{1}{3} *pi*1,5^2*2 sqrt{3} =1,5pi sqrt{3}$

V = 1,5π√3 см³ ≈ 8,2 см³

Приложения: