4 легких тригонометрических уравнения (10 класс)
фото внутри!
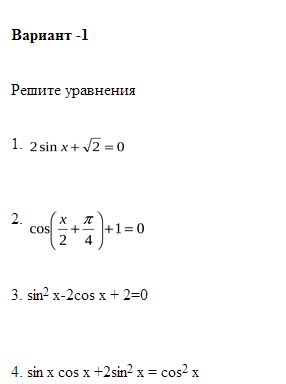
Ответы
sinx=-V2/2 (-1)^n*arcsin(-v2/2) +pi n x=(-1)^(n+1) *pi/4 +pi n
COS(X/2+PI/4)=-1 x/2+pi/4=pi +2pi n x/2=pi-pi/4+2pi n x/2=3pi/4 +2pi n
x=3pi/2+4pi n
sin^2x-2cosx+2=0 1-cos^2x-2cosx+2=0 -cos^2x-2cosx+3=0 D=4+12=16
cosx=(2-4)/(-2) =1 x=2pi n
cosx=(2+4)/(-2)=-3 не бывает
sinxcosx+2sin^2x=cos^2x поделим на cos^2x tgx+2tg^2x=1 2tg^2x+tgx-1=0
tgx=(-1-3)/4=-1 x=-pi/4 +pi n
tgx=1/2 x=arctg1/2 +pi n
№1
2sinx+√2=0
2*(sinx+√22)=0
sinx+√22=0
sinx=-√22
x=(-1)^n*arcsin(-√22)+pi*n
x=
№2
cos(x2+pi4)+1=0
cos(x2+pi4)=-1
x2+pi4=pi+2*pi*n
x2=pi-pi4+pi*n
x2=3*pi4+pi*n
x=3*pi2+2*pi*n
№3
sin^2(x)-2cos(x)+2=0
1-cos^2(x)-2cos(x)+2=0
3-cos^2(x)-2cos(x)=0
cos^2(x)+2cos(x)-3=0
D=4-4*(-3)=4+12=16
cos(x)=-2±4
2
cos(x)=-3 или cos(x)=1
нет решений x=2*pi*n
№4
sin(x)*cos(x)+2*sin^2(x)=cos^2(x)
2*sin^2(x)+sin(x)cos(x)-cos^2(x)=0
Разделим все члены уравнения на cos^2(x)
2*tg^2(x)+tg(x)-1=0
D=1+8=9
tg(x)=-1±3
4
tg(x)=-1 или tg(x)=0,5
x=arctg(-1)+pi*n x=arctg(0,5)+pi*n
x=-pi4+pi*n
Во всех случаях n-целое число
Ответы выделены