Предмет: Алгебра,
автор: ilonaiermilova
Решите пожалуйста) буду очень благодарна)
Приложения:
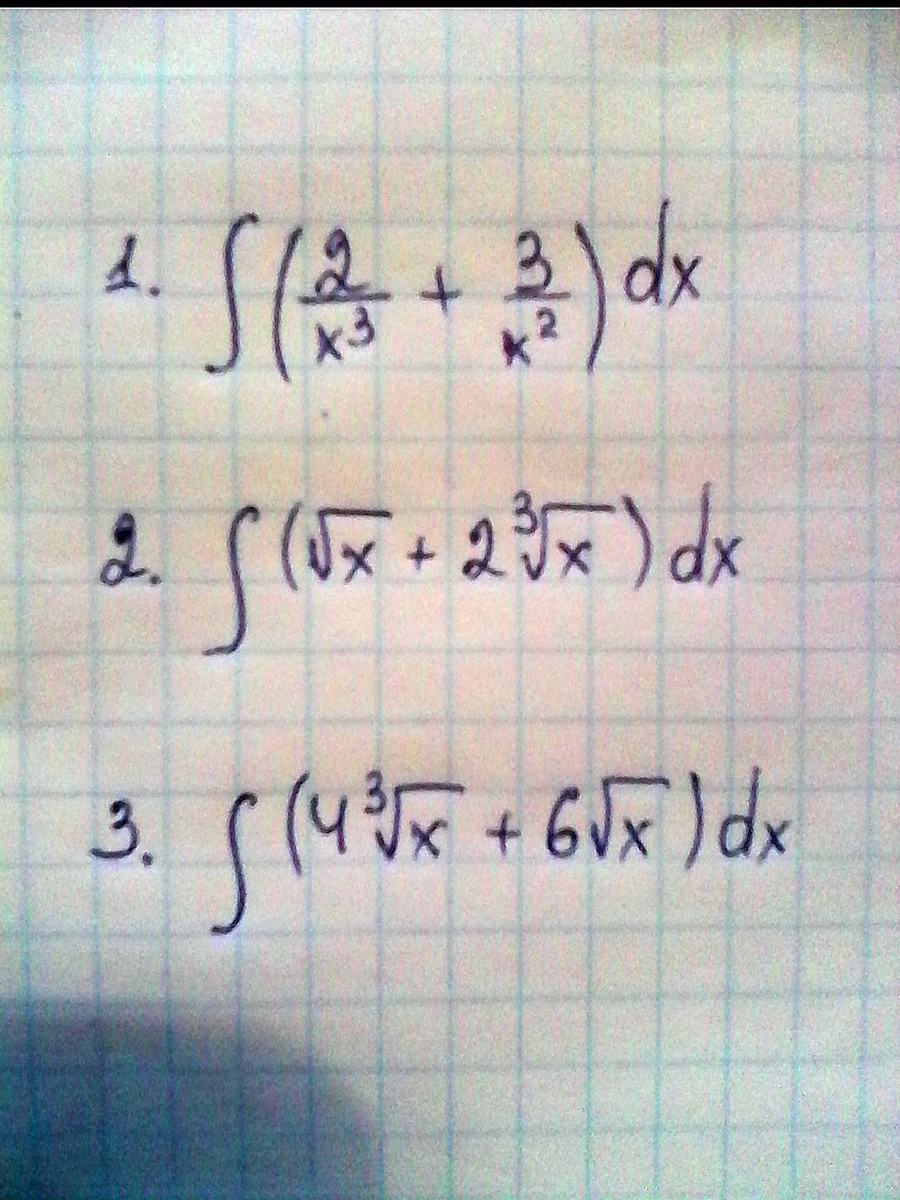
Ответы
Автор ответа:
1
Все ищется через первообразную
![\int\limits {(x^{ \frac{1}{2}}+2\cdot x^{ \frac{1}{3} }) }} \, dx = \frac{ x\sqrt[3]{x} (4 \sqrt[6]{x} +9) }{6} +C](https://tex.z-dn.net/?f=+%5Cint%5Climits+%7B%28x%5E%7B+%5Cfrac%7B1%7D%7B2%7D%7D%2B2%5Ccdot+x%5E%7B+%5Cfrac%7B1%7D%7B3%7D+%7D%29+%7D%7D+%5C%2C+dx+%3D++%5Cfrac%7B+x%5Csqrt%5B3%5D%7Bx%7D+%284+%5Csqrt%5B6%5D%7Bx%7D+%2B9%29+%7D%7B6%7D+%2BC "\int\limits {(x^{ \frac{1}{2}}+2\cdot x^{ \frac{1}{3} }) }} \, dx = \frac{ x\sqrt[3]{x} (4 \sqrt[6]{x} +9) }{6} +C")
![\int\limits {(4 \sqrt[3]{x}+6 \sqrt{x} ) } \, dx = \int\limits {(4x^{ \frac{1}{3}}+6x^{0.5}) }} \, dx =4x^{ \frac{3}{2} }+3x ^{\frac{4}{3}}+C](https://tex.z-dn.net/?f=+%5Cint%5Climits+%7B%284+%5Csqrt%5B3%5D%7Bx%7D%2B6+%5Csqrt%7Bx%7D+%29+%7D+%5C%2C+dx+%3D+%5Cint%5Climits+%7B%284x%5E%7B+%5Cfrac%7B1%7D%7B3%7D%7D%2B6x%5E%7B0.5%7D%29+%7D%7D+%5C%2C+dx+%3D4x%5E%7B+%5Cfrac%7B3%7D%7B2%7D+%7D%2B3x+%5E%7B%5Cfrac%7B4%7D%7B3%7D%7D%2BC "\int\limits {(4 \sqrt[3]{x}+6 \sqrt{x} ) } \, dx = \int\limits {(4x^{ \frac{1}{3}}+6x^{0.5}) }} \, dx =4x^{ \frac{3}{2} }+3x ^{\frac{4}{3}}+C")
Автор ответа:
2
Решение во вложении))))))))
Приложения:
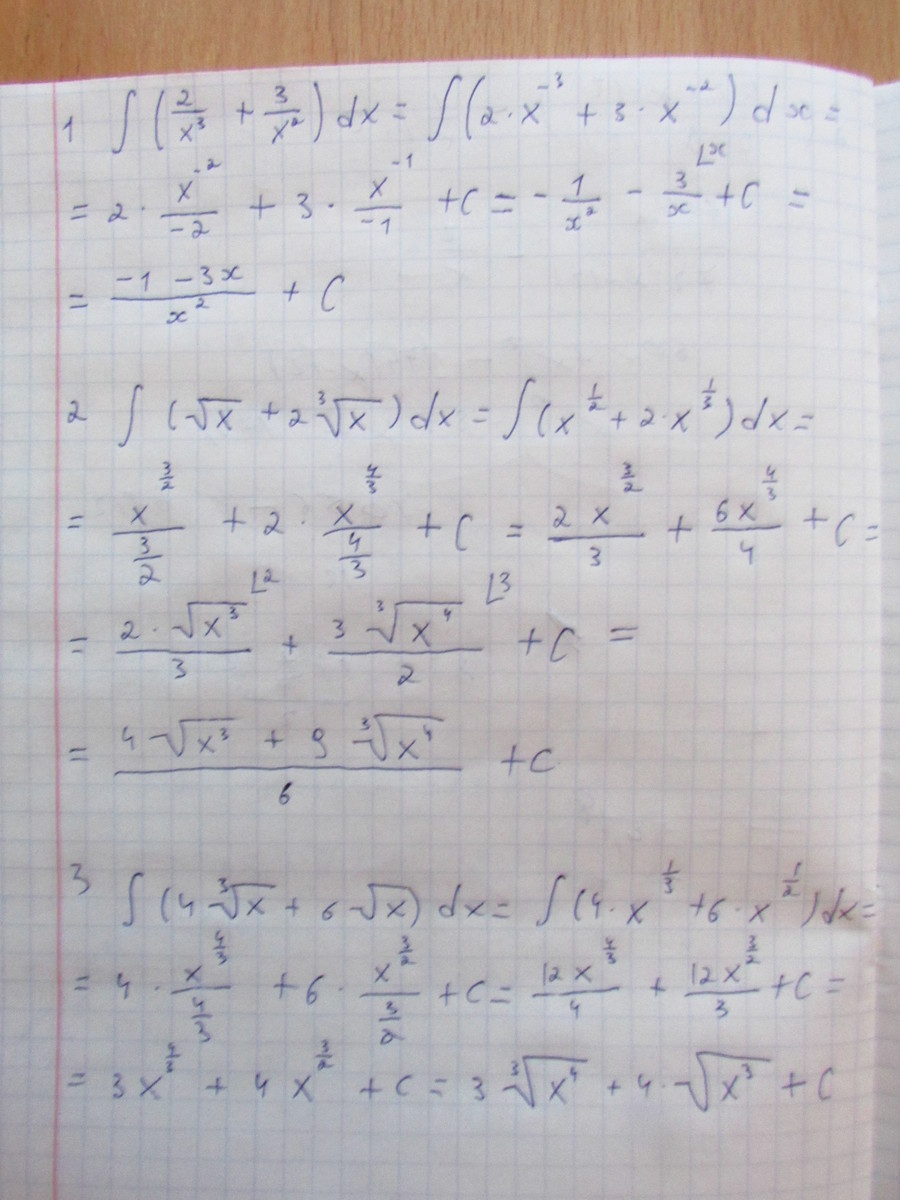
Интересные вопросы
Предмет: Українська мова,
автор: Panda328
Предмет: Русский язык,
автор: nikverevvv
Предмет: Українська мова,
автор: 170708
Предмет: География,
автор: 0437894