Докажите что медиана треугольника разбивает его на два треугольника одинаковой площади

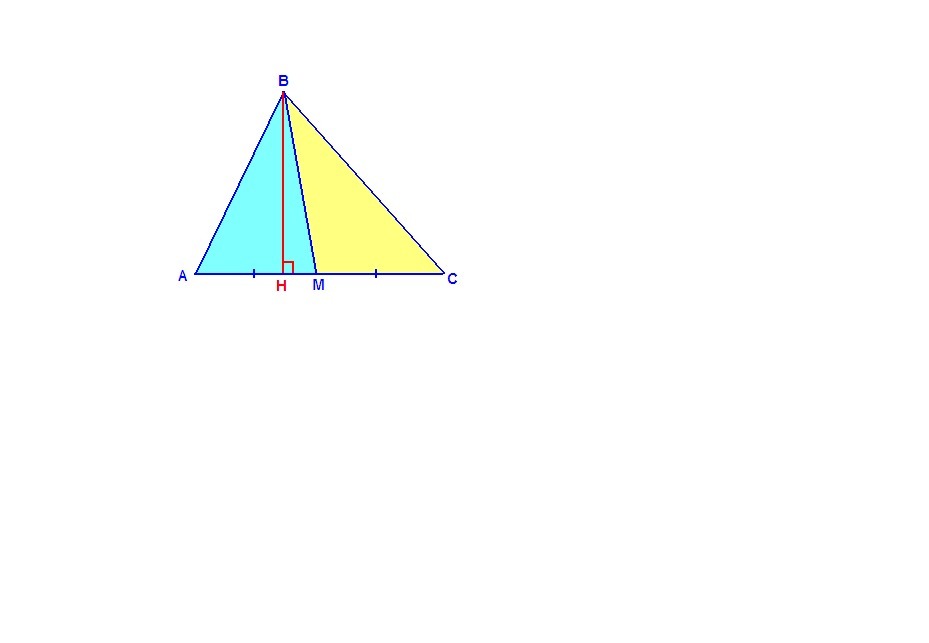
Пусть дан треугольник АВС, ВМ - медиана.
Тогда АМ = МС.

Проведем высоту ВН.
ВН является высотой как треугольника АВМ, проведенной к основанию АМ, так и треугольника СВМ, проведенной к основанию СМ.

Площадь треугольника находится как половина произведения стороны на проведенную к ней высоту. Значит,

Sabm = 1/2 · AM · BH
Scbm = 1/2 · CM · BH
но АМ = СМ, значит и

Sabm = Scbm

Что и требовалось доказать.