Найдите площадь боковой поверхности правильной шестиугольной пирамиды со стороной основания 4 см и высотой 2 см. (ответ должен получиться 48 см(в квадрате)

 

 

 

h=2sqrt(3) высота основания

l=sqrt(4*3+4)=4 -апофема

S=6*4*4/2=16*3=48

Площадь боковой поверхности правильной шестиугольной пирамиды равна площади 6-ти равнобедренных треугольников с основанием, равным стороне основания пирамиды и высотой, равной апофеме.
Т.е.
Площадь боковой поверхности правильной шестиугольной пирамиды равна половние произведения апофемы на периметр основания.

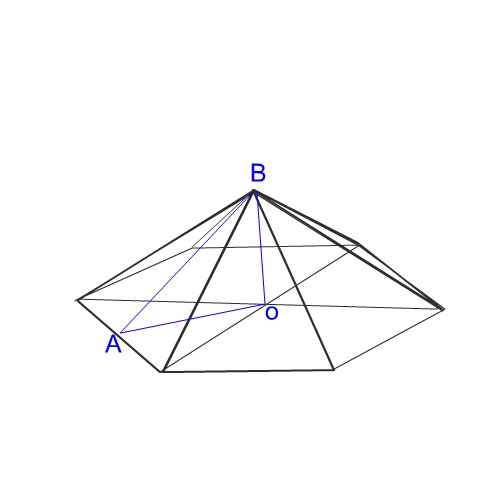
Апофему найдем из треугольника АВО, где ВО - высота пирамиды, АО- радиус вписанной в шестиугольник окружности. Он равен высоте равностороннего треугольника, из которых состоит основание.  
ВО=2,
АО==а(√3):2=4(√3):2=2√3
Апофема
АВ=√(АО²+ВО²)=√16=4
S бок=6·4·4:2=48 см²