Предмет: Геометрия, автор: GMLV

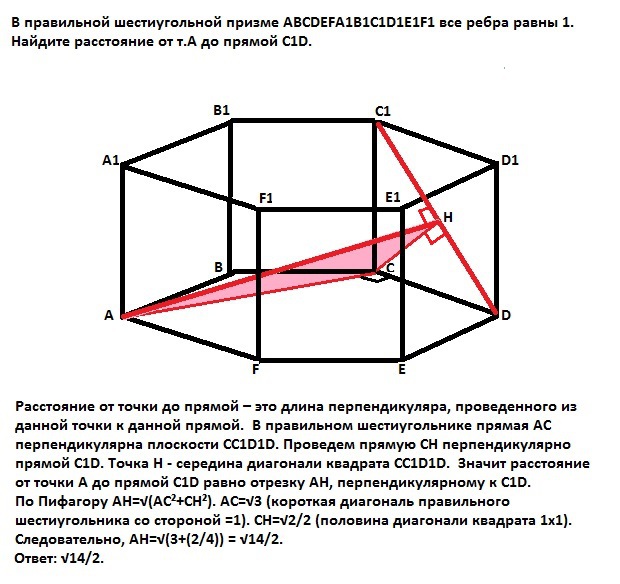
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1.Найдите расстояние от т.А до прямой C1D

Ответы

Автор ответа: Andr1806

Расстояние от точки до прямой – это длина перпендикуляра, проведенного из данной точки к данной прямой. В правильном шестиугольнике прямая АС перпендикулярна плоскости СС1D1D. Проведем прямую СН перпендикулярно прямой С1D. Точка Н - середина диагонали квадрата СС1D1D. Значит расстояние от точки А до прямой С1D равно отрезку АН, перпендикулярному к С1D.
По Пифагору АН=√(АС²+СН²). АС=√3 (короткая диагональ правильного шестиугольника со стороной =1). СН=√2/2 (половина диагонали квадрата 1х1).
Следовательно, АН=√(3+(2/4)) = √14/2.
Ответ: √14/2.

Приложения:

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Английский язык, автор: 0банана0

Scott Cory sounds just like an ordinary 13-year-old kid. His accent is pure southern Californian and his favoured description of pretty much anything is simple: 'cool'.

Yet Scott is a genius. He is the 'wunderkind' of the climbing world, who as a teenager has already mastered some of the planet's toughest climbs. Many expect him one day to be hailed as the world's greatest natural rock climber in a sport for the superfit and very brave. Not that that bothers Scott. 'It is really fun. It's cool,' he told The Observer.
Scott Cory sounds just like an ordinary 13-year-old kid. His accent is pure southern Californian and his favoured description of pretty much anything is simple: 'cool'.
Yet Scott is a genius. He is the 'wunderkind' of the climbing world, who as a teenager has already mastered some of the planet's toughest climbs. Many expect him one day to be hailed as the world's greatest natural rock climber in a sport for the superfit and very brave. Not that that bothers Scott. 'It is really fun. It's cool,' he told The Observer.

Scott is one of a number of ever younger athletes in the United States. They include a six-year-old weightlifter and a 14-year-old football professional. They have raised worries about the welfare of youngsters thrust into the limelight at a tender age.

Scott already holds numerous records, including being the youngest climber to scale the peaks of Half Dome and El Capitan in Yosemite National Park: among the most famous 'big wall' climbs in the world. The ascent on Half Dome usually takes top adult climbers three days. Scott did it in one.

Now he is planning a charity climb of both peaks within 24 hours. He will climb a total of 4,900 feet of rock - almost four times the height of the Empire State Building.

Scott got his first commercial endorsement deal at the age of eight. Now, among many other sponsors, North Face pays for him to travel to climb and supplies him with its equipment. Despite going to school every day, he is already a professional athlete in one of the world's most dangerous sports.

Tyanna Madsen, aged six, created a storm this month when she deadlifted 45 kilogrammes in a competition. She became involved in the sport at three.

Despite health experts - including the American Pediatric Association - warning that children lifting weights can put their health at risk, Tyanna's achievements, which could put her in the Guinness Book of Records, have caused a media frenzy second only to that surrounding 14-year-old soccer player Freddy Adu. Last week the boy became the youngest professional in a top-level American sport for more than 100 years.

Freddy, whose parents are from Ghana, will play with professional Washington football team DC United next season.

'We wanted to allow him to pursue his dreams and develop his God-given talents. As he makes this next step at the age of 14, it was best for him to stay in America,' said Freddy's mother, Emelia. Offers from European clubs, including Manchester United, had been rejected, she said. Media pundits compare Freddy's talent to that of Brazilian genius Pele.

Scott's parents want their son to keep studying and to see a possible future outside climbing.

'He has a brother and a sister who keep him down to earth real easy. They tell him all the time how useless he is,' joked his proud father Jim.

2 года назад

Предмет: Русский язык, автор: AntiHype228

Запишите по оброзцу.
Пример: Считают-считаешь, считает;
И так-же сделать с этими глаголами:
Делили, тянут, косили,скачут,пололи,искали,видят,ду-мают,варила,жарила,возят,дремлют,
Стояли,копал,прячут,начинали,зябнут,
Пускают,просили,моют,машут,писали,
Сидят.

Обозначьте спряжения глаголов и проверте их личные окончания по инфинетиву.

2 года назад

Предмет: Русский язык, автор: damirlevin7

Подготовьте устное публичное выстурление о происхождении имени Дамир