большая диагональ ромба равна 40 см,а меньшая диагональ относится к стороне как 6:5. найдите сторону и высоту ромба. помогите пожалуйста!!!! должно получится 25см и 24 см,а как это сделать не знаю(

 

Диагонали ромба перпендикулярны и точкой пересечения делятся пополам.
Пусть х - коэффициент  пропорциональности.
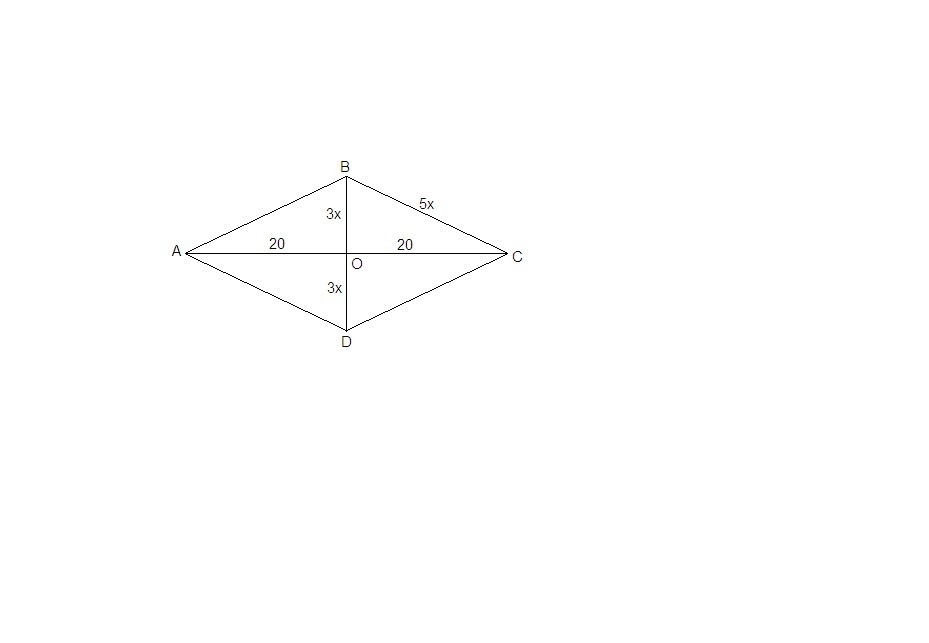
Тогда BD = 6х, AB = BC = CD = DA = 5x.
ВО = OD = 3х.
ΔВОС: ∠ВОС = 90°, по теореме Пифагора
           ВС² = ВО² + ОС²
           25x² = 9x² + 400
           16x² = 400
           x² = 25
           x = 5        (x = - 5 не подходит по смыслу задачи)
Сторона ромба: ВС = 5 · 5 = 25 см
BD = 6 ·5 = 30 см

Площадь ромба можно найти как половину произведения диагоналей или как произведение стороны на проведенную к ней высоту:
Sabcd = AC·BD/2 = BC·h, где h - высота ромба.
40 · 30 / 2 = 25 · h
h = 600/25 = 24 см