Предмет: Алгебра,
автор: kheymo
Помогите пожалуйста решить )25 баллов
Приложения:
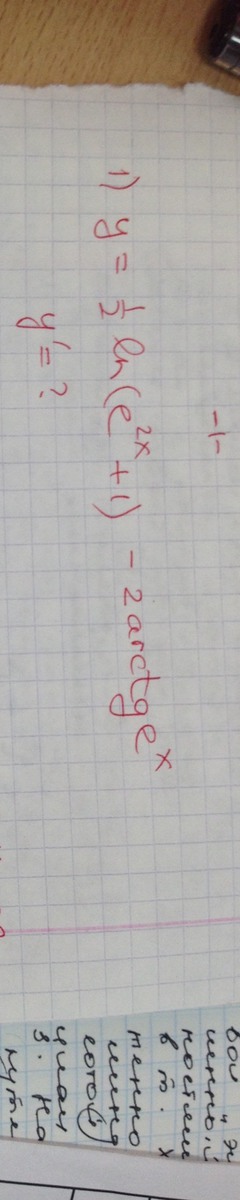
Ответы
Автор ответа:
1
y ' =(1/2Ln(e^(2x)+1) -2arctq(e^x )) ' = (1/2Ln(e^(2x)+1)) ' -(2arctq(e^x )) ' =
1/2*(Ln(e^(2x)+1)) ' -2(arctq(e^x )) ' =
(1/2(e^(2x)+1))*(e^(2x)+1) ' -(2*1/(1+(e^x )² ) *(e^x)'=
(1/2(e^(2x)+1))*(e^(2x)*(2x+1) ' -2e^x/ (1+(e^2x ) =
(1/2(e^(2x)+1))*(e^(2x)*2 -2e^x/ (1+(e^2x ) =
e^(2x)/(e^(2x)+1)) -2e^x/ (1+(e^2x ) .
ответ : y ' = e^(2x)/(e^(2x)+1)) -2e^x/ (1+(e^2x ) .
1/2*(Ln(e^(2x)+1)) ' -2(arctq(e^x )) ' =
(1/2(e^(2x)+1))*(e^(2x)+1) ' -(2*1/(1+(e^x )² ) *(e^x)'=
(1/2(e^(2x)+1))*(e^(2x)*(2x+1) ' -2e^x/ (1+(e^2x ) =
(1/2(e^(2x)+1))*(e^(2x)*2 -2e^x/ (1+(e^2x ) =
e^(2x)/(e^(2x)+1)) -2e^x/ (1+(e^2x ) .
ответ : y ' = e^(2x)/(e^(2x)+1)) -2e^x/ (1+(e^2x ) .
Интересные вопросы
Предмет: Қазақ тiлi,
автор: джиги07770
Предмет: Українська мова,
автор: maria11sw1
Предмет: Беларуская мова,
автор: AToMiC000
Предмет: Математика,
автор: amajstrenko2007
Предмет: Физика,
автор: hakobyanarman2004