Предмет: Геометрия,
автор: Velogonschik
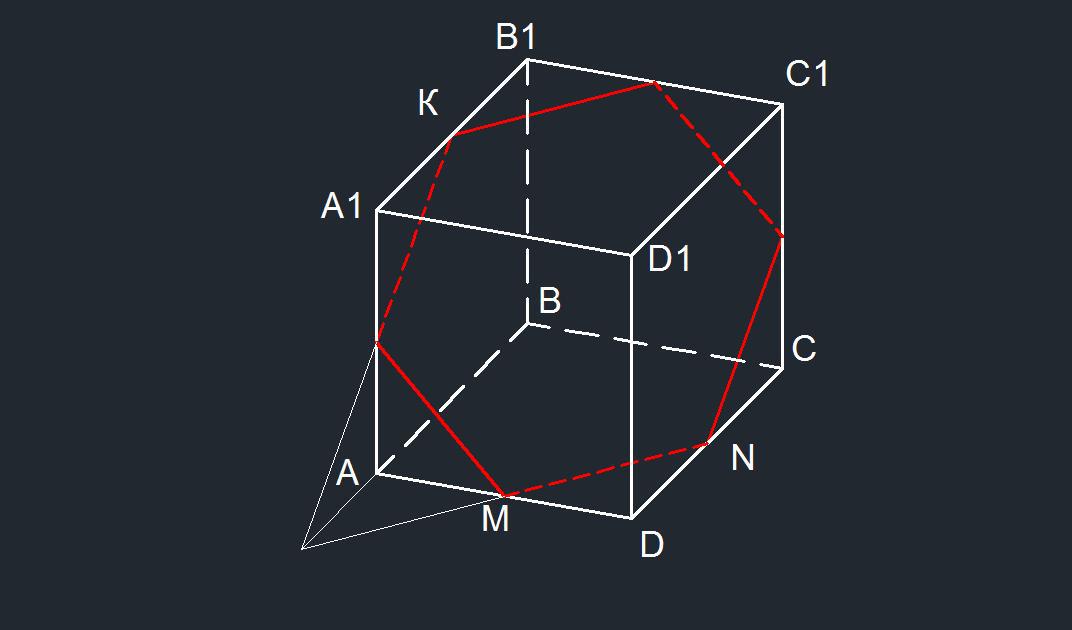
В кубе ABCDA1B1C1D1 отмечены точки M N и K - середины ребер AD, CD, A1B1 соответственно.
Найдите площадь сечения куба плоскостью MNK, если ребро куба равно 6.
Ответы
Автор ответа:
3
сечение - правильный шестиугольник со стороной =(1/2)√(6²+6²)=3√2
Sсеч=6*SΔ
S=6*((3√2)² *√3)/4
Sсеч=27√3
Sсеч=6*SΔ
S=6*((3√2)² *√3)/4
Sсеч=27√3
Приложения:
Velogonschik:
спасибо
Автор ответа:
2
В сечении образуется правильный шестиугольник.
Сторона равна 3√2 как гипотенуза равнобедренного прямоугольного треугольника.
Площадь правильного шестиугольника S = (3√3a²) / 2=
= 3√3*18 / 2 = 27√3 кв.ед.
Сторона равна 3√2 как гипотенуза равнобедренного прямоугольного треугольника.
Площадь правильного шестиугольника S = (3√3a²) / 2=
= 3√3*18 / 2 = 27√3 кв.ед.
Приложения:
спасибо
Интересные вопросы
Предмет: Русский язык,
автор: goldwildcat1
Предмет: Окружающий мир,
автор: rang23
Предмет: Беларуская мова,
автор: настя7206
Предмет: Геометрия,
автор: Letiravi
Предмет: Английский язык,
автор: yoove