Предмет: Математика, автор: nina481

20 баллов+10 ПОМОГИТЕ РЕШИТЬ ( с рисунком и подробнее)
В равнобедренную трапецию с острым углом 60⁰ вписана окружность радиуса 8. Найдите длину диагонали трапеции.

Матов: перезагрузи страницу если не видно

nina481: Я НЕ ТУ ЗАДАЧУ ВЫЛОЖИЛА

nina481: ВАМ СПАСИБО ЗА РЕШЕНИЕ

nina481: Хотя нет, и эту тоже нужно.

Ответы

Автор ответа: Матов

Значит выполняется условие вписанности окружности в трапецию ,
$AB+CD=2BC\\$ , опустим высоту $BH$ , из прямоугольного треугольника $\Delta BHC$ $BC=\frac{BH}{sin60}\\ BH=BCsin60 = \frac{\sqrt{3}BC}{2}\\$
Но так как $CD=2CH+AB$ , можно выразить из того же прямоугольного треугольника $\Delta BHC$ , $CH=\frac{BC}{2}\\$
Значит
   $CD=BC+AB\\ BC+2AB=2BC\\ AB=\frac{BC}{2}\\$
Но радиус равен
$BH=2r \\ \frac{\sqrt{3}}{4}*BC=8\\ BC=\frac{32}{\sqrt{3}}\\ AB=\frac{16}{\sqrt{3}}\\$

Откуда диагональ $AC= \sqrt{AB^2+BC^2-2*AB*BC*cos(90а+30а) }\\ AC= \frac{16\sqrt{21}}{3}$

Приложения:

Предыдущий вопрос

Следующий вопрос

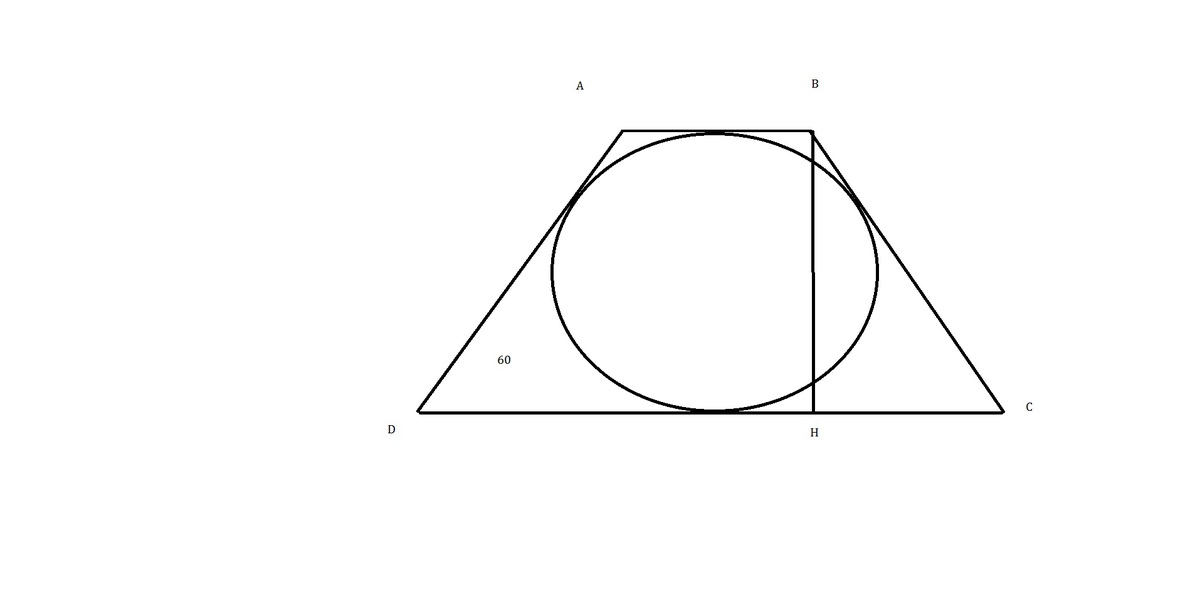
Интересные вопросы

Предмет: Русский язык, автор: ника2552

Подскажите название сказок?

2 года назад

Предмет: Английский язык, автор: ПппоротныйКирилл

какой город России я б хотел посетить и почему

2 года назад

Предмет: Русский язык, автор: dgmhrrjfethd

Составить предложение по схеме:
[определенно-личное],союз И [безличное].

20 баллов+10 ПОМОГИТЕ РЕШИТЬ ( с рисунком и подробнее) В равнобедренную трапецию с острым углом 60⁰ вписана окружность радиуса 8. Найдите длину диагонали трапеции.

Ответы

20 баллов+10 ПОМОГИТЕ РЕШИТЬ ( с рисунком и подробнее)
В равнобедренную трапецию с острым углом 60⁰ вписана окружность радиуса 8. Найдите длину диагонали трапеции.