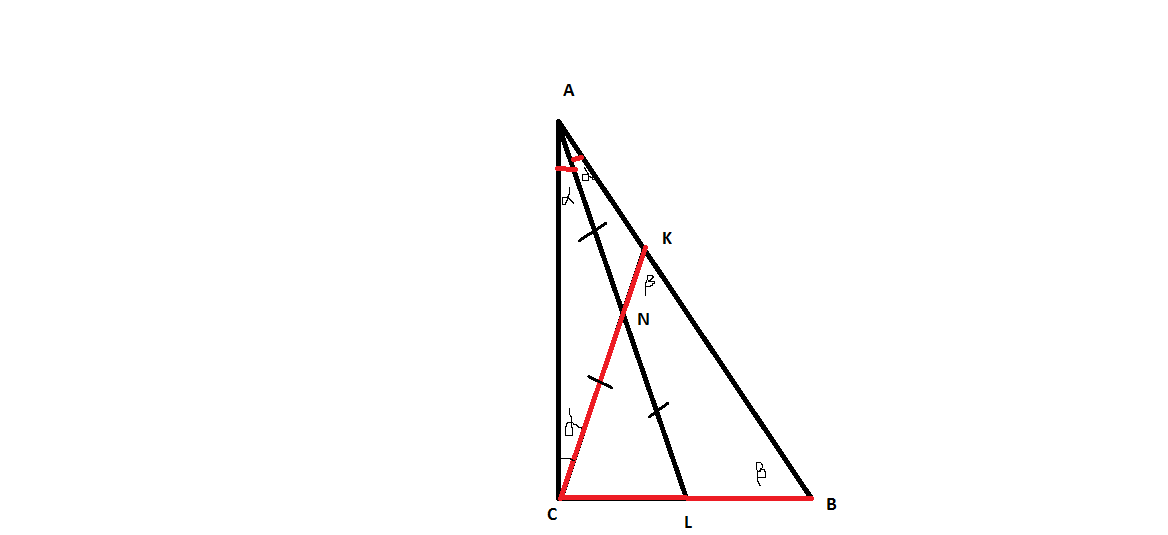
На гипотенузе AB прямоугольного треугольника ABC , выбрана точка K , для которой CK=BC. Отрезок CK пересекает биссектрису AL в ее середине. Найдите углы треугольника ABC.

см. рисунок. думаю, будет понятно. Задачка , вроде, не трудная.
итак, СК=СВ  - треуг. ВСК равнобедр, углы при его основании равны. Я их обозначил
AL- биссектриса, то равные углы я обозначил как

АN=NL значит, т. N для прямоуг.треугольника ACL является центром описанной окружности, значит, AN=NL=NC  , значит, треуг. ANC равнобедренный, и углы при основании равны  , и равны
тепиерь, угол СКВ внешний для треуг. АКС, значит угол СКВ==
из прямоуг. треуг. АВС      угол А+угол В=90