Предмет: Математика,
автор: vazovsky339
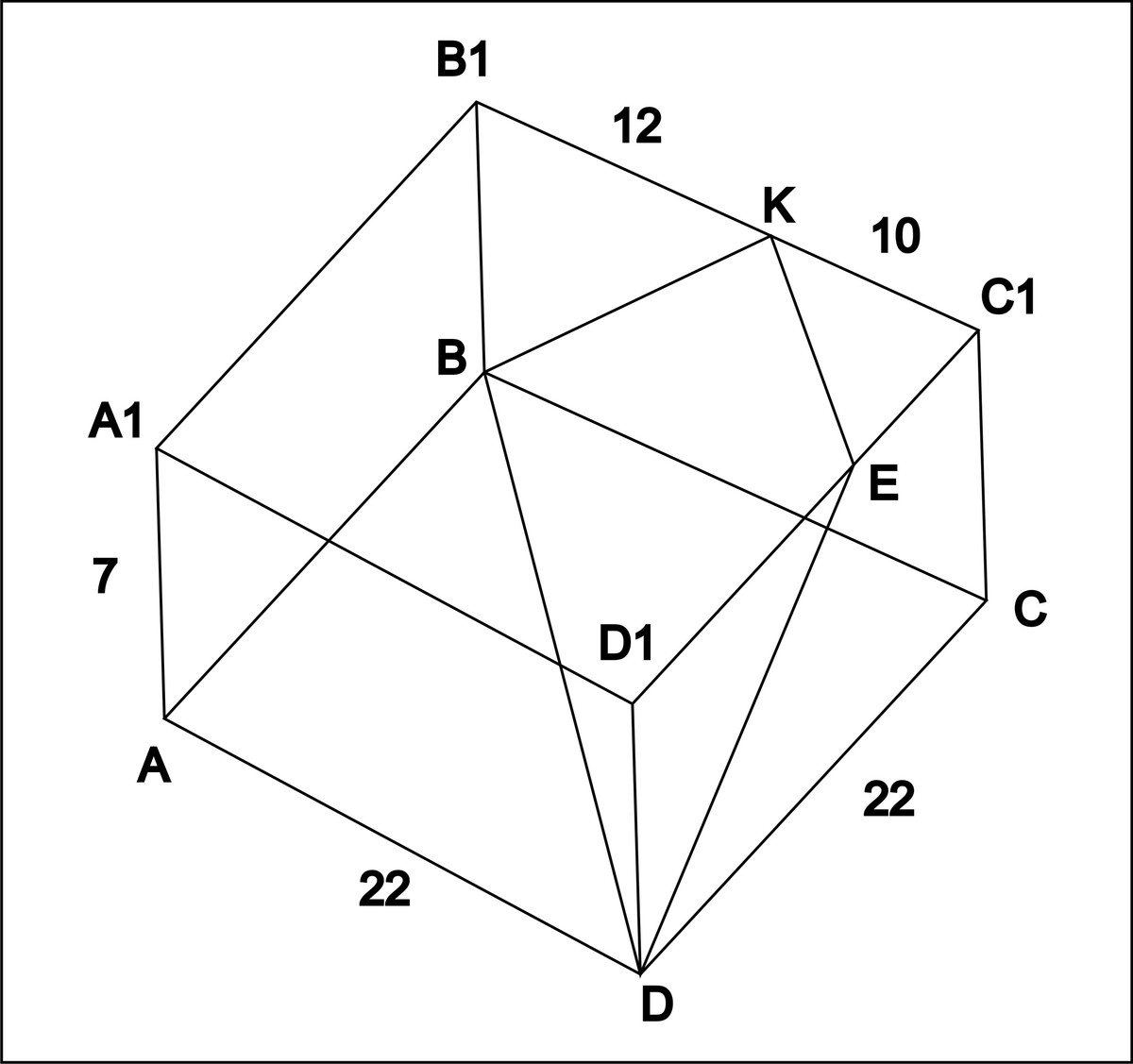
в правильной четырёхугольной призме abcda1b1c1d1 сторона основания равна 22, а боковое ребро AA1=7.точка K принадлежит ребру B1C1 и делит его в отношении 6:5, считая от вершины B1. Найдите площадь сечения этой призмы плоскостью, проходящая через точки B, D и K
Ответы
Автор ответа:
8
плоскости ABCD и A₁B₁C₁D₁ параллельны, значит при пересечении их третьей плоскостью образуются параллельные прямые BD и KE
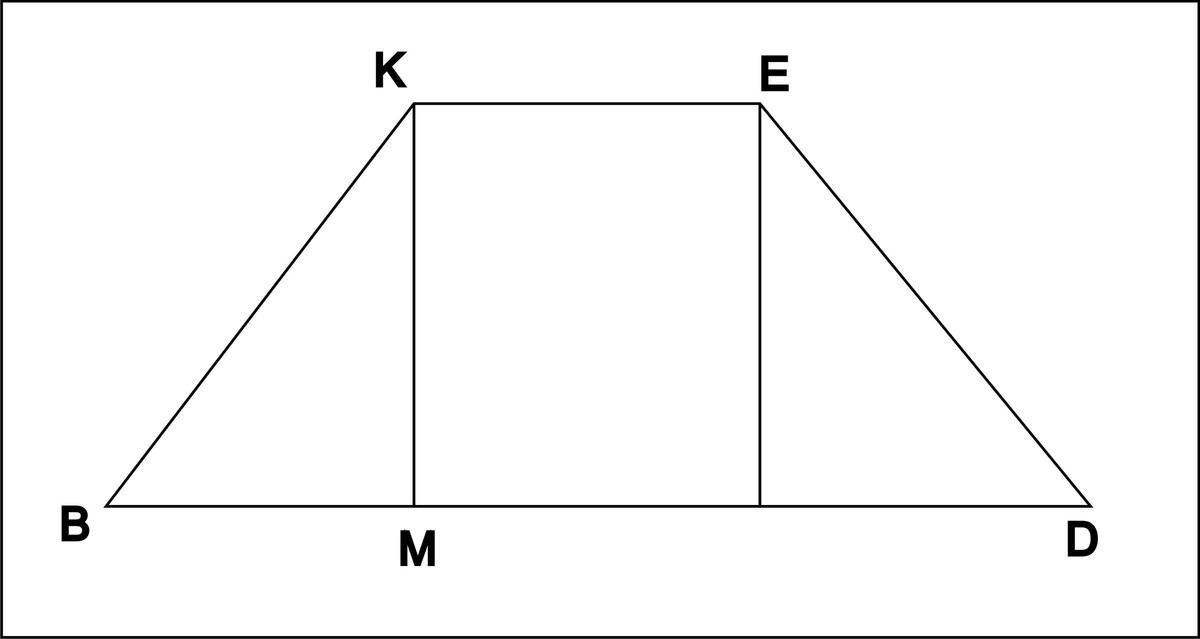
BKED- равнобокая трапеция
по теореме Пифагора
BD²=AD²+AB²=968
BD=22√2
KE²=KC₁²+EC₁²=200
KE=10√2
DE=BK
BK²=B₁K²+B₁B²
BK=√193
BM=(BD-KE)/2=(√968-√200)/2
KM²=BK²-BM²=193-72=121
KM=11
S(трапеции)=((BD+KE)/2)·KM=((22√2+10√2)/2)·11=176√2
Ответ:176√2
BKED- равнобокая трапеция
по теореме Пифагора
BD²=AD²+AB²=968
BD=22√2
KE²=KC₁²+EC₁²=200
KE=10√2
DE=BK
BK²=B₁K²+B₁B²
BK=√193
BM=(BD-KE)/2=(√968-√200)/2
KM²=BK²-BM²=193-72=121
KM=11
S(трапеции)=((BD+KE)/2)·KM=((22√2+10√2)/2)·11=176√2
Ответ:176√2
Приложения:
Интересные вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: azalia2017
Предмет: Українська мова,
автор: Keoni
Предмет: Математика,
автор: guss53