Предмет: Геометрия, автор: fdsdfasd

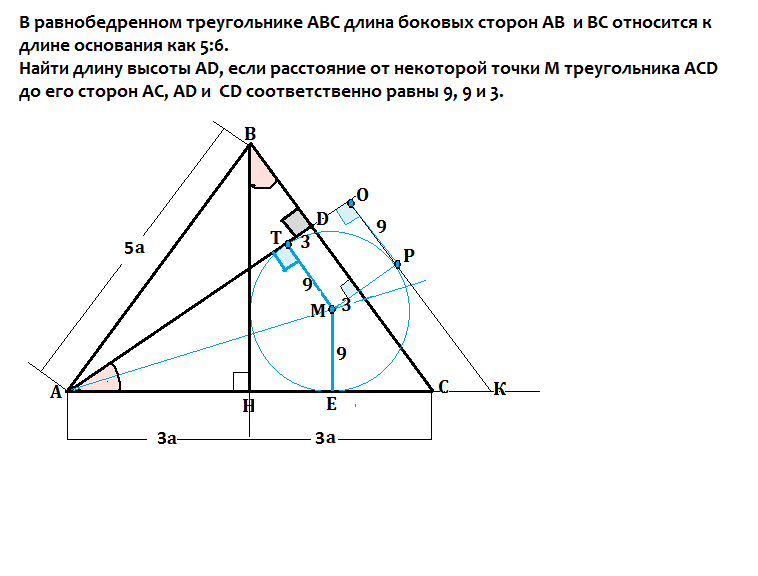
в равнобедренном треугольнике ABC длина боковых сторон AD и BC относится к длине основания AC как 5:6 .найти длину высоты AD , если расстояния от некоторой точи M треугольника ACD до его стороны AC, AD и CD соответственно равны 9, 9, и 3

Ответы

Автор ответа: Hrisula

Опустим из В высоту на АС.
В прямоугольном тр-ке ВСН отношение катета НС к гипотенузе ВС=3:5. ⇒ тр-к ВНС - египетский, и НС:ВН:ВС=3:4:5. ( можно проверить т.Пифагора)
Расстояние от точки до прямой измеряется длиной перпендикулярного к ней отрезка.
Так как расстояние от М до сторон АD и АС одинаково, то по свойству биссектрисы угла точка М лежит на биссектрисе угла DАС и является центром вписанной в этот угол окружности с радиусом МТ=МЕ=9.
Нарисуем эту окружность.
Проведем радиус МР как продолжение перпендикуляра из М к DС. Проведем через Р касательную ОК.
ОК||МТ⇒ OK|| DC, треугольник АОК - прямоугольный и подобен треугольнику АDС.
В то же время тр-к АDС подобен треугольнику ВНС - оба прямоугольные с общим углом С. ⇒
Треугольник АОК - подобен тр-ку ВНС и ОК:АО:АК=3:4:5
Пусть коэффициент этого отношения будет х.
Тогда ОК=3х, АО=4х, АК=5х
ОР=ТМ=ТО=МР=R=9
Формула радиуса вписанной в прямоугольный треугольник окружности
r=(а+b-c):2 , где a и b- катеты, с - гипотенуза.
18=3х+4х-5х ⇒
х=9
АО=4*9=36
В треугольнике АОК отрезок ДО=ТО-ТД=9-3=6
АD=36-6=30

Приложения: