Предмет: Математика, автор: CioOrAn

Постройте график функции f(x) = $left { {{-x^2-4x-4} atop {1-|x-1|}} right.$ Если для первого &x<-1,а для второго &x > или равно -1 и найдите при каких значениях параметра а он имеет равно 2 общие точки с прямой y=a

Ответы

Автор ответа: arsenlevadniy

0

$f(x)=left { {{-x^2-4x-4, x textless -1;} atop {1-|x-1|, xgeq-1;}} right. \ -x^2-4x-4=-(x^2+4x+4)=-(x+2)^2; \ x-1lessgtr0, xlessgtr1, \ -1 leq x textless 1, 1-|x-1|=1+(x-1)=x, \ x geq 1, 1-|x-1|=1-(x-1)=-x+2; \ f(x)= left { begin{array}{c}-(x+2)^2, x textless -1,\x, -1leq x textless 1,\-x+2, xgeq1;end{array}right.$
$ain(-infty;-1)cup(0;1)$

Приложения:

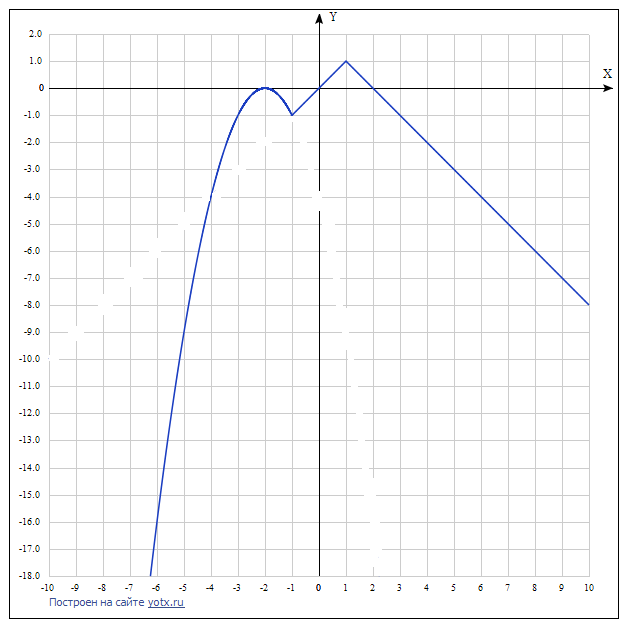
Автор ответа: CioOrAn

0

Что означает 3 строка

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Українська мова, автор: Аноним

міні-твір на тему школа з використанням дієприслівниковими зворотами. швидко!!!!!!
поможіть даю 100 балів

6 лет назад

Предмет: Биология, автор: milena250811

ребят,у нас рисование дистанционно и дают темы на дом. сегодня сказали нарисовать свободную тему,чтобы можно было повесить на стену в коридоре,но рисовать над не праздники,а я не знаю что нарисоватьПомогите, пожалуйста!!

6 лет назад

Предмет: Английский язык, автор: pingvin7639

1 they didnt (say, tell, tolk, to speak) her anything
2 you never(say, tell, tolk, to speak) me anything
3. could you (say, tell, tolk, to speak)your name please
4 i am afraid i dont know (say, tell, tolk, to speak)

6 лет назад

Предмет: Химия, автор: vlasov154

Сколько грамов CuO образуется при раазложении 196 грамов Cu(OH)2

10 лет назад

Предмет: Математика, автор: Олесечка2003

сумма трёх чисел 3100.первое слагаемое наибольшее трёхзначное число,второе наименьшее четырёхзначное число.чему равно третье слагаемое?(Без x,y)-(без икстов)!!!

10 лет назад