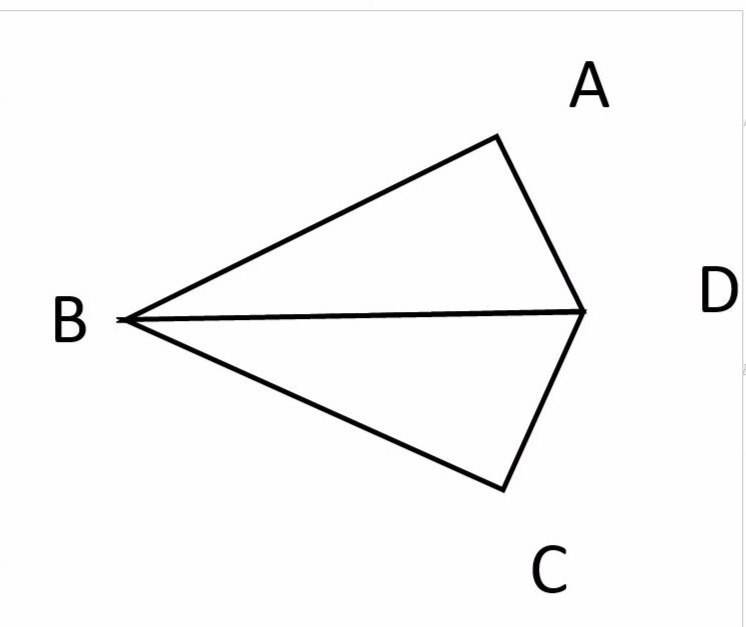
1. Доказать, что , если АВ = CВ, угол АВD равен углу DBC.

Пусть в четырехугольнике АВСD стороны АВ и СD паралельны и АВ=СD. Проведем диагональ АС, разделяющую данный четырехугольник на два треугольника АВС и СDА. Эти треугольники равны по двум сторонам и углу между ними (АС- общая сторона, АВ=СD по условию, <1=<2 как накрест лежащие углы при пересечении параллельных прямых АВ и СD cекущей АС), поэтому <3=<4 . Но углы 3 и 4 накрест лежащие при пересечении прямых АD и ВС секущей АС, следовательно, АD парелелен ВС. Таким образом, в четырехугольнике АВСD противоположные стороны попарно параллельны, и, значит, четырехугольник АВСD- параллелограмм, а значит угл АВD не равен углу DВС