11 КЛАСС ПОМОГИТЕ ПОЖАЛУЙСТА!!!
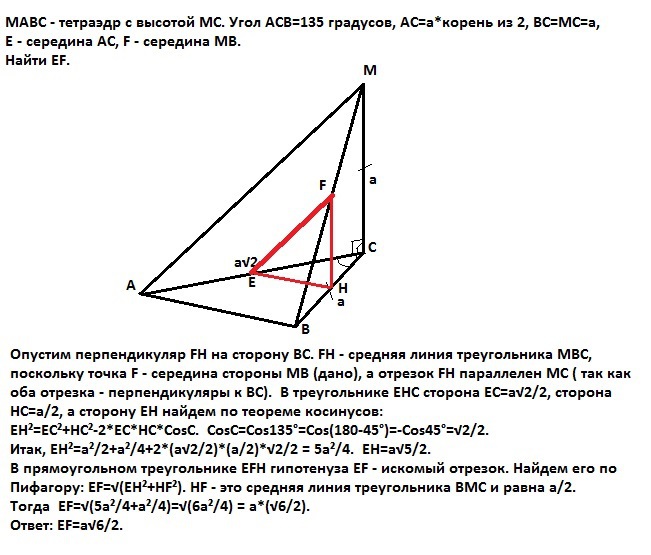
MABC - тетраэдр с высотой MC. Угол ACB=135 градусов, AC=a*корень из 2, BC=MC=a, E - середина АС, F - середина MB. Найти EF.

Опустим перпендикуляр FH на сторону ВС. FH - средняя линия треугольника МВС, поскольку точка F - середина стороны МВ (дано), а отрезок FH параллелен МС (так как оба отрезка - перпендикуляры к ВС). 
В треугольнике ЕНС сторона ЕС=а√2/2, сторона НС=а/2, а сторону ЕН найдем по теореме косинусов:
ЕН²=ЕС²+НС²-2*ЕС*НС*CosC.  CosC=Cos135°=Cos(180-45°)=-Cos45°=√2/2.
Итак, ЕH²=a²/2+a²/4+2*(а√2/2)*(а/2)*√2/2 = 5a²/4.  ЕН=а√5/2.
В прямоугольном треугольнике EFH гипотенуза EF - искомый отрезок. Найдем его по Пифагору: EF=√(EH²+HF²). HF - это средняя линия треугольника ВМС и равна а/2.
Тогда  EF=√(5a²/4+a²/4)=√(6a²/4) = а*(√6/2).
Ответ: EF=а√6/2.