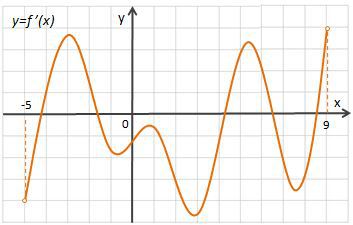
На рисунке изображен график производной функции y = f(x) , определенной на интервале (–5; 9).
Найдите количество точек, в которых касательная к графику функции y = f(x) параллельна прямой y= - 2x-31 или совпадает с ней.

Таких точек 5 .
Так как касательная параллельна прямой у=-2х-31, то
угловой коэффициент касательной будет совпадать с
угловым коэффициентом прямой  у=-2х-31, который равен
коэффициенту перед переменной х, то есть  к=-2.
 Но    .  Поэтому надо найти количество  точек
пересечения графика f '(x) с прямой у=-2. Таких точек 5.