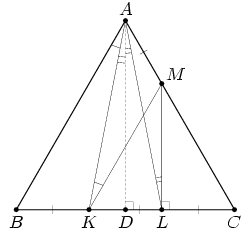
На стороне BC равностороннего треугольника ABC отмечены точки K и L так, что BK = KL = LС, а на стороне AC отмечена точка M так, что AM = 1/3 AC. Чему равна сумма углов AKM и ALM?

Из того, что треугольник АВС равносторонний следует, что АМ=ВК, а значит и треугольник МКС — равносторонний и тогда ∠MCK=60°. Опустив высоту треугольника МКС из точки М увидим, что она, с одной стороны, является медианой ∠KМС, а с другой стороны — параллельна высоте AD треугольника ABC поэтому ∠АLМ=∠LАD. D – середина отрезка KL, значит, треугольник KAL – равнобедренный; тогда его высота AD является и биссектрисой, следовательно ∠LАD=∠KАD. Отсюда вытекает, что ∠АKМ+∠АLМ=∠KАВ+∠KАD=∠BАD= 30°.