Предмет: Геометрия,
автор: BJIADA
В равностороннем треугольнике ABC со стороной a проведена высота BD. Вычислите скалярное произведение векторов:
а) AB*AC; б) AC*CB; в) AC*BD; г) AC*AC
Ответы
Автор ответа:
0
Скалярное произведение двух векторов равно произведению модулей этих векторов на косинус угла между ними.
а)

По условию все стороны треугольника равны а, а все углы равностороннего треугольника равны 60 градусов:

б)

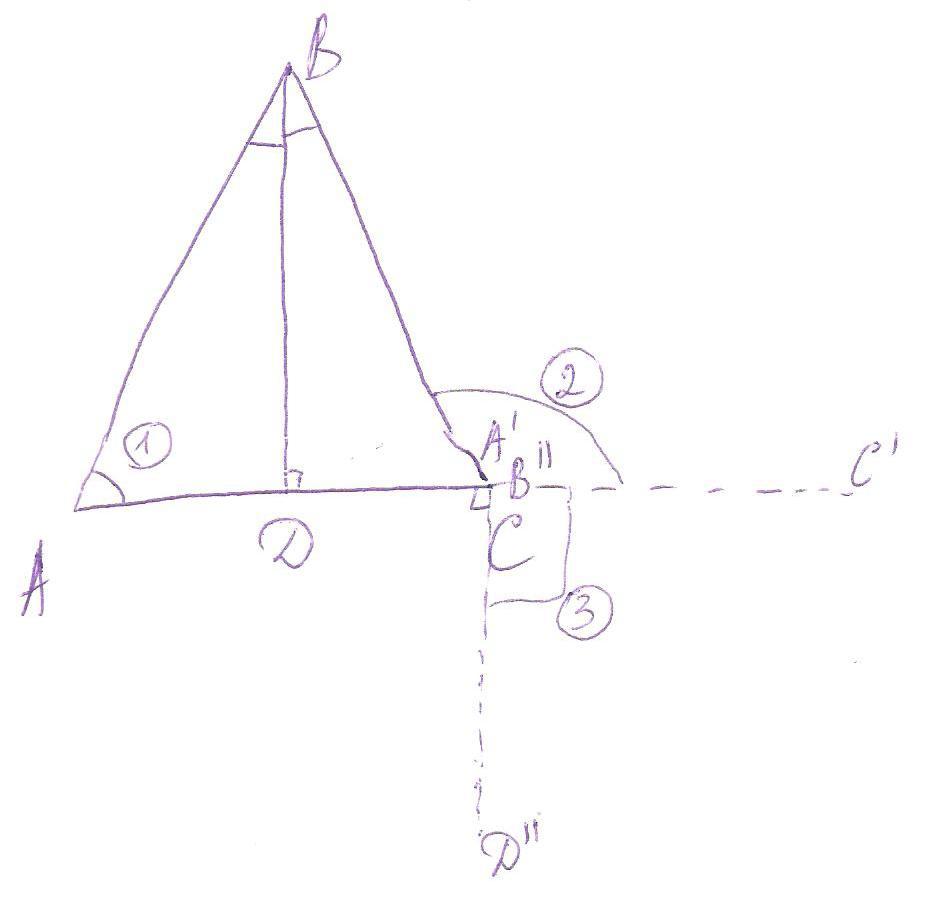
Чтобы определить угол между векторами АС и СВ нужно совместить их начала, например, перенести параллельным переносом вектор АС так, чтобы точка А совместилась с точкой С. Тогда будет видно, что углом между этими векторами будет угол, смежный с углом АСВ, равный 180-60=120 градусов:

в)

Так как BD высота к АС, то векторы ВD и АС перпендикулярны, скалярное произведение перпендикулярных векторов равно 0:

г)
Произведение вектора само на себя (скалярный квадрат) равно квадрату его модуля, угол в данном случаем между одним и тем же вектором равен нулю:

а)
По условию все стороны треугольника равны а, а все углы равностороннего треугольника равны 60 градусов:
б)
Чтобы определить угол между векторами АС и СВ нужно совместить их начала, например, перенести параллельным переносом вектор АС так, чтобы точка А совместилась с точкой С. Тогда будет видно, что углом между этими векторами будет угол, смежный с углом АСВ, равный 180-60=120 градусов:
в)
Так как BD высота к АС, то векторы ВD и АС перпендикулярны, скалярное произведение перпендикулярных векторов равно 0:
г)
Произведение вектора само на себя (скалярный квадрат) равно квадрату его модуля, угол в данном случаем между одним и тем же вектором равен нулю:
Приложения:
Интересные вопросы
Предмет: Химия,
автор: dbrazinskaa
Предмет: Алгебра,
автор: QWERTYRUSSIA
Предмет: Другие предметы,
автор: brainle230
Предмет: Математика,
автор: anna230873
Предмет: Литература,
автор: malishka3004