Предмет: Геометрия,
автор: mandrygina19
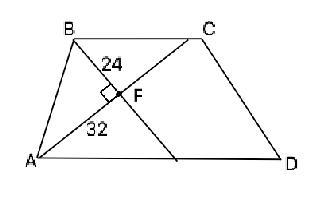
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F . Найдите AB, если AF=24, BF=32 ?
Ответы
Автор ответа:
0
Ответ: 40 (ед. длины)
Объяснение:
Основания трапеции параллельны, боковые стороны при них - секущие, поэтому сумма внутренних углов трапеции при боковой стороне равна 180°.
Биссектрисы этих углов делят их пополам, следовательно, сумма этих половин 180°:2=90°. ⇒ В ∆ AFB из суммы углов треугольника ∠AFB=180°-90°=90°. ∆ АВF - прямоугольный. По т.Пифагора АВ=√(AF²+BF²)=√(24²+32²)=40 (ед. длины)
Приложения:
Интересные вопросы
Предмет: Биология,
автор: xSqeazy
Предмет: История,
автор: aya11asem
Предмет: Математика,
автор: Аноним
Предмет: География,
автор: mrxondar
Предмет: Математика,
автор: epluskova