Предмет: Алгебра, автор: Malkom

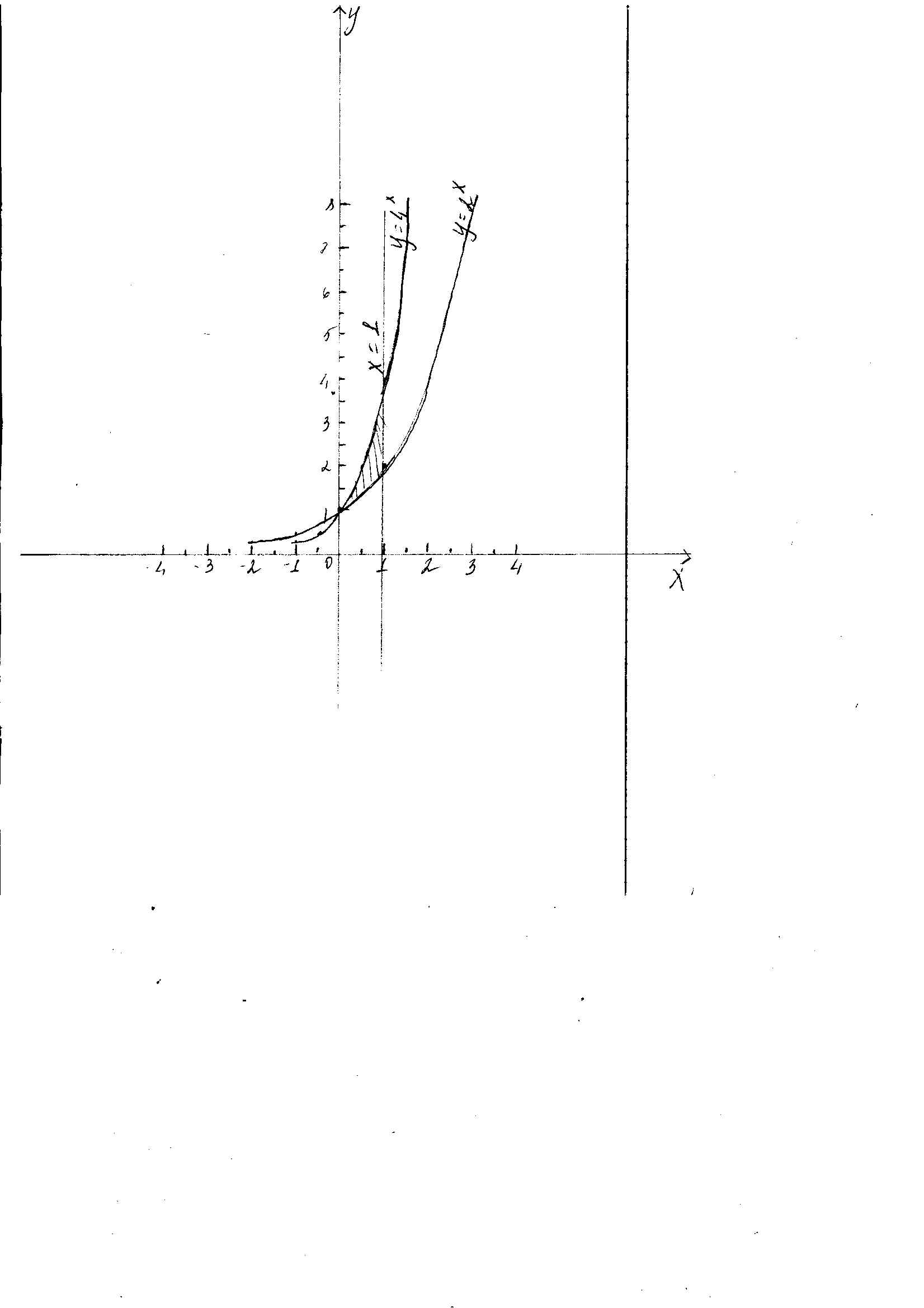
Найти площадь фигуры, огранниченной линиями y=2^x, y=4^x, x=1

Ответы

Автор ответа: midory

0

Как видно из рисунка который я приложила к решению нужно найти площадь заштрихованной фигуры. Площадь это интеграл, по х от 0 до 1 верхняя граница это 4^х нижняя - 2^x. То есть площадь выражается: $S=intlimits^1_0 {4^{x}-2^{x}} , dx=intlimits^1_0 {4^{x}} , dx-intlimits^1_0 {2^{x}} , dx=\\ =frac{4^{x}}{ln4}|^1_0-frac{2^{x}}{ln2}|^1_0=frac{4^{1}}{ln4}-frac{4^{0}}{ln4}-frac{2^{1}}{ln2}+frac{2^{0}}{ln2}=frac{4}{2ln2}-frac{1}{2ln2}-frac{2}{ln2}+frac{1}{ln2}=\\ =frac{4-1-4+2}{2ln2}=frac{1}{2ln2}$

Приложения:

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Английский язык, автор: kenzhayupovaramina

The______ are here childThe

7 лет назад

Предмет: История, автор: snegannakz

чем занималились люди в каменном веке

7 лет назад

Предмет: Литература, автор: fuchizhimargo57

сроооооочноооо пожалуйста 20баллов даю

7 лет назад

Предмет: Геометрия, автор: Аноним

в прямоугольном треугольнике a и b -катеты найдите:a)b,если а=8,с=12 б)с,если а=4в корне 2,b=7 в)а,еслиb=3 в корне три,с=5 вкорне три

10 лет назад

Предмет: Геометрия, автор: manynia23

периметр правильного треугольника, вписанного в окружность, равен 18 см. найдите сторону квадрата, вписанного в ту же окружность.

10 лет назад