Вычислить площадь фигуры ограниченной линиями y=x3 y=8 x=1

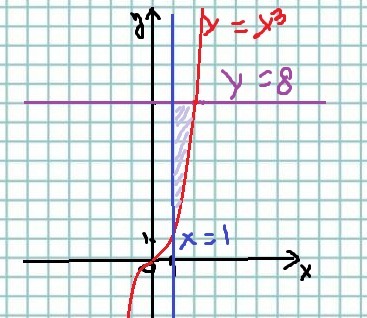
Сначала необходимо построить график (см. рисунок), и определиться, какая площадь искомая. В нашем случае, это часть плоскости от 1 до 2, сверху ограниченная кубической параболой , а снизу - прямой у=8. Значит, при интегрировании мы будем вычитать из функции функцию  у=8. 



Ответ: 4,25.