Предмет: Алгебра,
автор: zhekaz
11 класс логорифмы, помогите
Приложения:
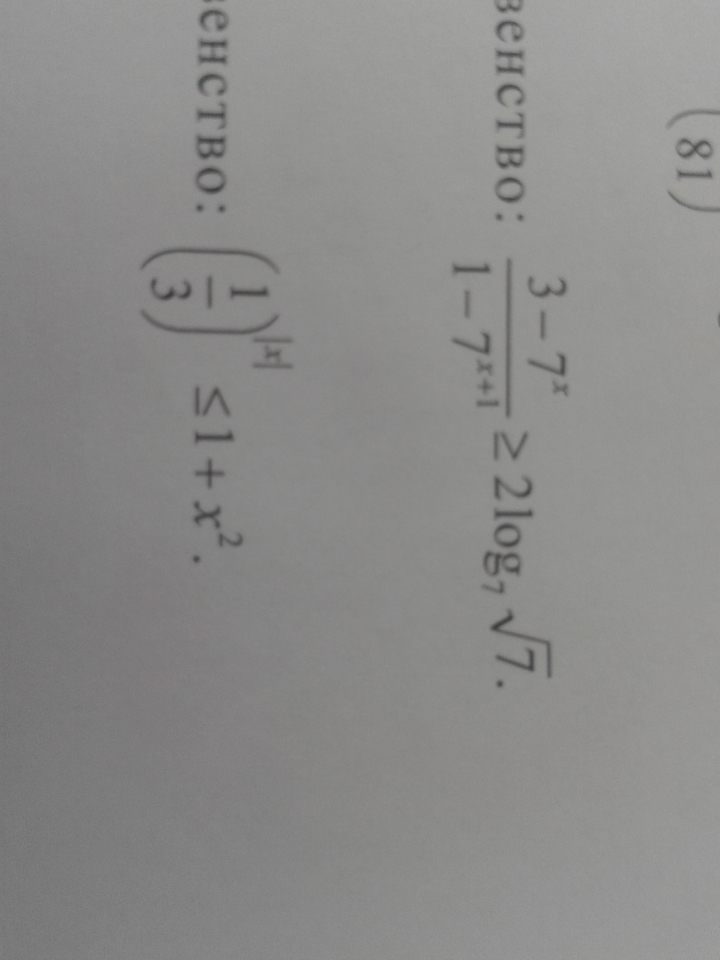
Ответы
Автор ответа:
0
(3-7^x)/(1-7^(x+1)≥2*log₇√7
(3-7^x)/(1-7*7^x)≥2*log₇7¹/²
(3-7^x)/(1-7*7^x)≥1
3-7^x≥1-7*7^x
6*7^x≥-2
7^x≥-1/3 ⇒
x∈(-∞;+∞).
(1/3)^IxI≤1+x²
Левая и правая части неравенства - чётные функции:
(1/3)^I-xI=(1/3)^x 1+(-x)²=1-x² ⇒
(1/3)^x≤1+x²
Так как 0<(1/3)^x≤1 ⇒
x∈(-∞;+∞).
(3-7^x)/(1-7*7^x)≥2*log₇7¹/²
(3-7^x)/(1-7*7^x)≥1
3-7^x≥1-7*7^x
6*7^x≥-2
7^x≥-1/3 ⇒
x∈(-∞;+∞).
(1/3)^IxI≤1+x²
Левая и правая части неравенства - чётные функции:
(1/3)^I-xI=(1/3)^x 1+(-x)²=1-x² ⇒
(1/3)^x≤1+x²
Так как 0<(1/3)^x≤1 ⇒
x∈(-∞;+∞).
Интересные вопросы
Предмет: Математика,
автор: satimendesh
Предмет: Английский язык,
автор: golibsuvonqulov
Предмет: Обществознание,
автор: Rikterka
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: НастяВасильеваmister