Предмет: Геометрия,
автор: kozyrev313
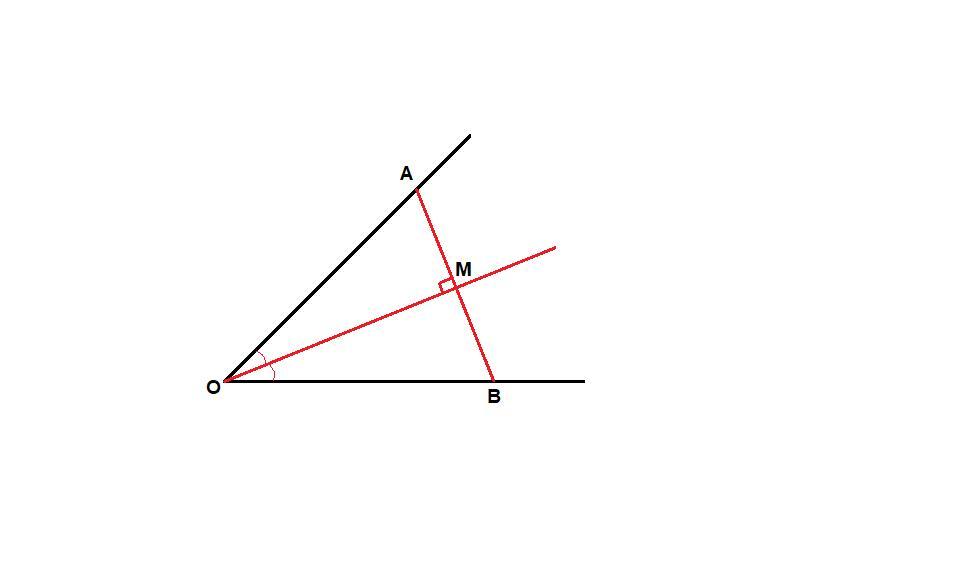
Через точку M, принадлежащую биссектрисе угла с вершиной в точке О, провели прямую, перпендикулярную биссектрисе. Эта прямая пересекает стороны данного угла в точках A и B. Докажите, что AM=MB.
Ответы
Автор ответа:
0
Объяснение:
∠АОМ = ∠ВОМ, так как ОМ биссектриса,
∠АМО = ∠ВМО = 90°, так как АВ ⊥ ОМ,
ОМ - общая сторона для треугольников АОМ и ВОМ, следовательно
ΔАОМ = ΔВОМ по катету и прилежащему острому углу (или по стороне и двум прилежащим к ней углам).
В равных треугольниках против равных углов лежат равные стороны, значит АМ = ВМ.
Приложения:
Интересные вопросы
Предмет: Қазақ тiлi,
автор: dentalsden87
Предмет: Химия,
автор: dlya73
Предмет: Математика,
автор: lolkakaxa22
Предмет: История,
автор: 5СчАсТлИвАя5
Предмет: Математика,
автор: XxXxWiZaRdXxXx