Предмет: Алгебра, автор: susha2001

Помогите пожалуйста!!) Нужно очень срочно с объяснением!

Приложения:

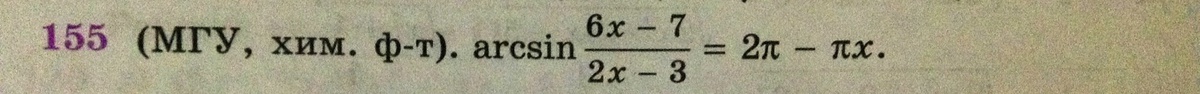
Ответы

Автор ответа: gartenzie

$arcsin{ frac{ 6x - 7 }{ 2x - 3 } } = 2 pi - pi x$ ;

ОДЗ:

$left{begin{array}{l} left|begin{array}{l} -frac{ pi }{2} leq 2 pi - pi x leq frac{ pi }{2} ; \\ -frac{1}{2} - 2 leq - x leq frac{1}{2} - 2 ; end{array}right \\ left|begin{array}{l} x neq 1.5 ; \\ | frac{ 6x - 7 }{ 2x - 3 } | leq 1 ; \\ frac{ | 6x - 7 | }{ | 2x - 3 | } leq 1 ; \\ | 6x - 7 | leq | 2x - 3 | ; end{array}right end{array}right$

$left{begin{array}{l} -0.5 + 2 leq x leq 0.5 + 2 ; \\ left|begin{array}{l} x < frac{7}{6} ; Rightarrow 6x - 7 geq 2x - 3 ; Rightarrow 4x geq 4 ; Rightarrow x in [ 1 ; frac{7}{6} ) ; \\ x in [ frac{7}{6} ; 1.5 ) ; Rightarrow 6x - 7 leq 3 - 2x ; Rightarrow 8x leq 10 ; Rightarrow x in [ frac{7}{6} ; 1.25 ] ; \\ x geq 1.5 ; Rightarrow 6x - 7 leq 2x - 3 ; Rightarrow 4x leq 4 ; Rightarrow x in emptyset ; end{array}right end{array}right$

$left{begin{array}{l} x in ( 1.5 ; 2.5 ] ; \ x in [ 1 ; 1.25 ] ; end{array}right$

$x in emptyset$ ;

О т в е т : нет решений.

Автор ответа: gartenzie

Простите. Не обратила внимание на вашу просьбу о комментариях.

Пояснения. ОДЗ – область допустимых значений.

Выражение стоящее внутри арксинуса не может по модулю превосходить единицу, потому что иначе функция арксинуса не определена.

Сам арксинус даёт значения, не превосходящие по модулю (п/2), а поэтому правая часть по модулю так же никак не может превосходить (п/2).

Отсюда и берутся оба условия.

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Биология, автор: dnemkova090

Помогите сделать сравнительную таблицу на тему: "Классификация Членистоногих"

6 лет назад

Предмет: Математика, автор: emesusya90

Пожалуйста решите номера 3 и 5 пожалуйста объясните и решите

6 лет назад

Предмет: Немецкий язык, автор: tobyadd

Помогите пожалуйста!

6 лет назад

Предмет: Химия, автор: Zhorka18

Гидроксид меди(2) реагирует с
1) NaOH
2) CaO
3) H2SO4
4) CO

9 лет назад

Предмет: Математика, автор: Мария15к2002

Для приготовления салата на 3 части огурцов берут 2 части редиса и 1 часть лука. Сколько потребуется граммов огурцов, чтобы приготовить 300 г салата ?

9 лет назад