Докажите, что в треугольнике медиана, проведенная к одной из его сторон, меньше полусуммы двух других сторон.

Пусть вмедианаНужно доказать, чтоПродолжим медианузаи на продолжении отложимТогда полученный четырехугольникбудет параллелограммом, так как его диагонали AD и ВС в точке пересечения делятся пополам, значит, BD = АС. К тому жеВсторона меньше суммы двух других сторон, то есть
Что и требовалось доказать

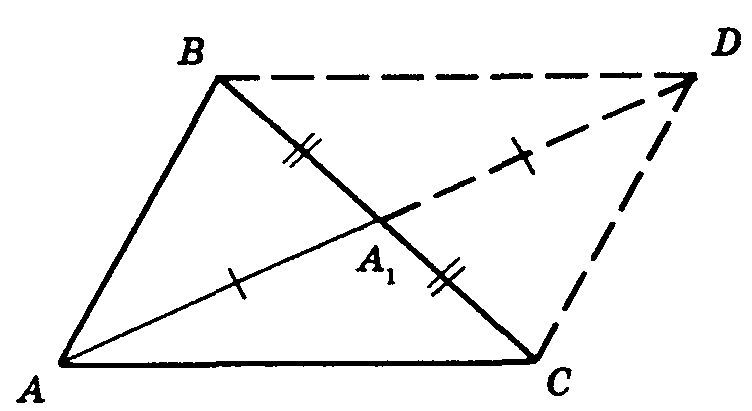
Продолжим медиану АА1 за А1 и на продолжении отложим А1D=AA1.Тогда полученный четырехугольник ABDC будет параллелограммом, так как его диагонали AD и ВС в точке пересечения делятся пополам, значит, BD = АС. К тому же AD = 2AA1 в треугольнике ABD сторона меньше суммы двух других сторон, то есть ПОЛУЧИМ : 

AD МЕНЬШЕ AB+BD. 2AA1 МЕНЬШЕ AB+AC.   

AA1 МЕНЬШЕ (ДРОБЬ) - ЧИСЛИТЕЛЬ ( AB+AC ) .ЗНАМЕНАТЕЛЬ ( 2 )