Предмет: Алгебра, автор: jassyflade

ОЧЕНЬ СРОЧНО
ПОМОГИТЕ РЕШИТЬ

Приложения:

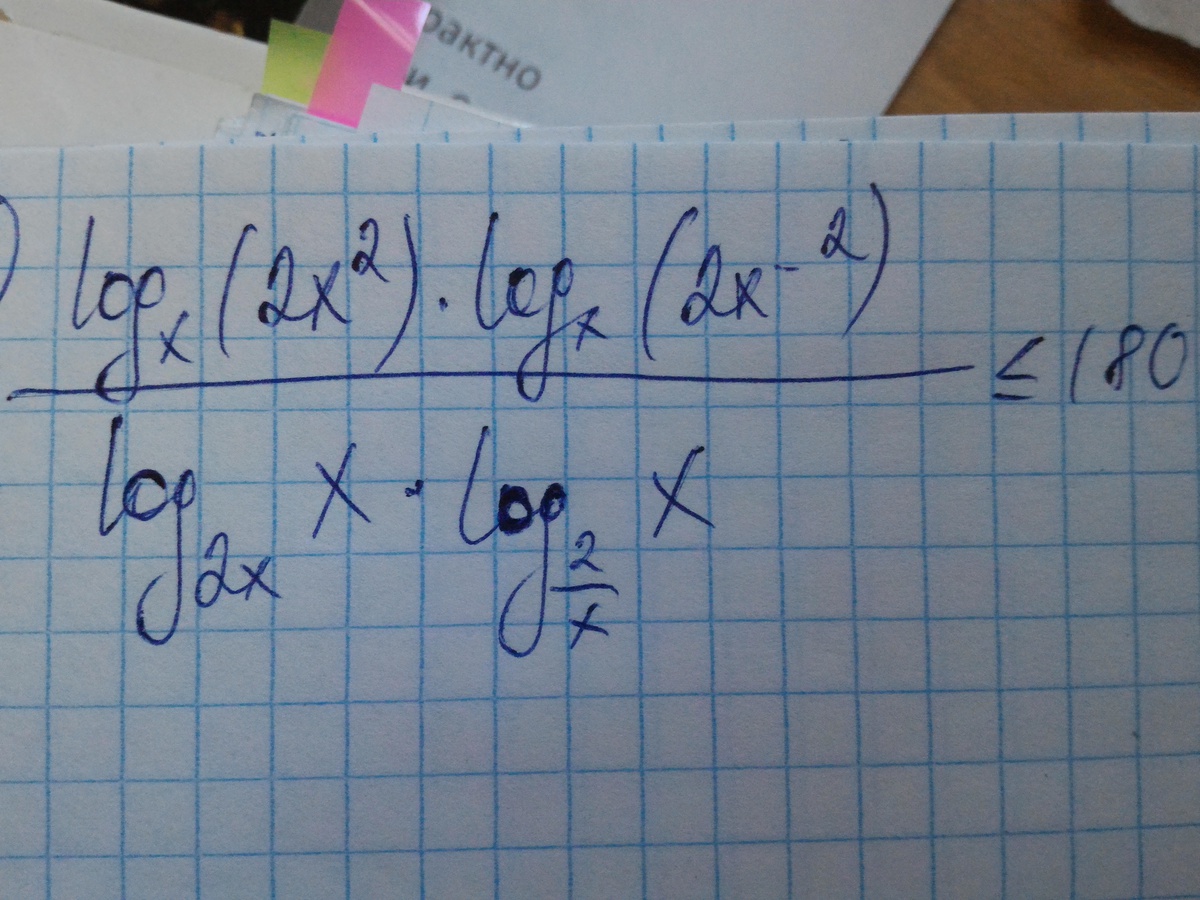
Ответы

Автор ответа: NNNLLL54

$frac{log_{x}(2x^2)cdot log_{x}(2x^{-2})}{log_{2x}xcdot log_{frac{2}{x}}x} leq 180\\ODZ:; x textgreater 0,xne 1,2xne 1,frac{2}{x}ne 1,; log_{2x}xcdot log_{frac{2}{x}}xne 0\\ frac{frac{lg(2x^2)}{lgx}cdot frac{lg(2x^{-2})}{lgx}}{frac{lgx}{lg(2x)}cdot frac{lgx}{lg(frac{2}{x})}} leq 180; ,; ; frac{(lg2+2lgx)(lg2-2lgx)(lg2+lgx)(lg2-lgx)}{lg^4x} leq 180\\\tak; kak; ; lg^4x geq 0,; to; \\(lg2+2lgx)(lg2-2lgx)(lg2+lgx)(lg2-lgx) leq 180lg^4x\\Zamena:; ; lg2=a; ,; lgx=t$

$(a+2t)(a-2t)(a+t)(a-t) leq 180t^4\\(a^2-4t^2)(a^2-t^2)-180t^4 leq 0\\a^4-5a^2t^2+4t^4-180t^4 leq 0\\176t^4+5a^2t^2-a^4 leq 0|:a^4ne 0\\176(frac{t}{a})^4+5(frac{t}{a})^2-1 leq 0; ,; ; (frac{t}{a})_{1,2}=frac{-5-sqrt{729}}{2cdot 176}\\(frac{t}{a})_1=-frac{1}{11}; ,; ; (frac{t}{a})_2=frac{1}{16}$

$-frac{1}{11} leq frac{t}{a} leq frac{1}{16}$

$-frac{1}{11} leq frac{lgx}{lg2} leq frac{1}{16}$

$a); ; frac{lgx}{lg2}=-frac{1}{11}; ,; ; lgx=-frac{1}{11}cdot lg2; ,; lgx=lg(2^{-frac{1}{11}}); ,; x=2^{-frac{1}{11}}=frac{1}{sqrt[11]{2}}$

$b); ; frac{lgx}{lg2}=frac{1}{16}; ,; lgx=frac{1}{16}cdot lg2; ,; lgx=lg(2^{frac{1}{16}}); ,; x=2^{frac{1}{16}}=sqrt[16]{2}$

$frac{1}{sqrt[11]2} leq x leq sqrt[16]2$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Русский язык, автор: aishapro67788

Запиши глаголы в 3-ем лице единственного числа, будущего времени с
указанной приставкой. Определи спряжение.
видеть - у
строить - по
бороться – по
клеить - пере
колоть - за

6 лет назад

Предмет: География, автор: demaanupriev12

Задание №2 Ответьте на вопросы:

1.Назовите древнейшую из мировых религий .

2.Назовите вторую по времени возникновения релгию.
3.Назовите религию, котораявключаетв себя три ветви: католицизм, протествнтизм и православие.

4.Назовите религию. Возникшую в VIIв. Среди населения Аравийского полуострова.

5.Назовите священную книгу мусульман.

6.Назовите религиозный центр всех мусульман.

7. Назовите священную книгу христианства.

6 лет назад

Предмет: Математика, автор: sultanabylay6

20,105:5 погите пажайлусьа

6 лет назад