Предмет: Математика,
автор: ivkin1998
вычислить производную высшего порядка заданной функции
Приложения:
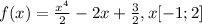
Ответы
Автор ответа:
0
Судя по заданию, здесь надо найти наибольшее и наименьшее значения функции на отрезке.
f(x) = x^4/2 - 2x + 3/2; x = [-1, 2]
Находим на концах отрезка
f(-1) = 1/2 - 2(-1) + 3/2 = 1/2 + 2 + 3/2 = 4
f(2) = 16/2 - 2*2 + 3/2 = 8 - 4 + 3/2 = 5,5
Находим точки экстремума. Производную приравниваем к 0.
f ' (x) = 4x^3/2 - 2 = 2x^3 - 2 = 2(x^3 - 1) = 0
x = 1
f(1) = 1/2 - 2*1 + 3/2 = 1/2 - 2 + 3/2 = 0
Наименьшее значение: f(1) = 0
Наибольшее значение f(2) = 5,5
f(x) = x^4/2 - 2x + 3/2; x = [-1, 2]
Находим на концах отрезка
f(-1) = 1/2 - 2(-1) + 3/2 = 1/2 + 2 + 3/2 = 4
f(2) = 16/2 - 2*2 + 3/2 = 8 - 4 + 3/2 = 5,5
Находим точки экстремума. Производную приравниваем к 0.
f ' (x) = 4x^3/2 - 2 = 2x^3 - 2 = 2(x^3 - 1) = 0
x = 1
f(1) = 1/2 - 2*1 + 3/2 = 1/2 - 2 + 3/2 = 0
Наименьшее значение: f(1) = 0
Наибольшее значение f(2) = 5,5
Автор ответа:
0
спасибо огромное)
Автор ответа:
0
Производные высших порядков: f''(x) = 6x^2; f'''(x) = 12x; f(iv)(x) = 12; f(v)(x) = 0
Интересные вопросы
Предмет: Русский язык,
автор: ptichkazloi
Предмет: История,
автор: ratmirkonihhev07
Предмет: Биология,
автор: dinaramurtazina79
Предмет: География,
автор: Оля148832