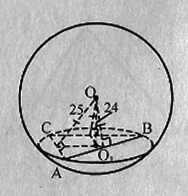
Сечение шара двумя параллельными плоскостями, между которыми лежит центр шара, имеют площади 144 (пи) и 25 (пи) квадратных см. Найдите площадь поверхности шара, если расстояние между параллельными плоскостями равно 17 см.

Находим радиусы окружностей в сечениях шара.
r1 = √(S/π) = √(25π/π) = 5 см,
r2 = √(144π/π) = 12 см.
Тогда расстояние между плоскостями будет складываться из двух катетов:
17² = (R² - 5²) + (R² - 12²).
289 = R² -25 + R² - 144.
2R² = 458.
R = √(458/2) = √229 ≈  15,13275 см (это радиус шара).
Получаем искомое значение:
Sшара = 4πR² =4π*229 = 916π ≈  2877,699 см².