диаметр основания конуса равен 6см,образующая наклонена к плоскости основания под углом 60 градусов.найти обьем шара описанного около конуса

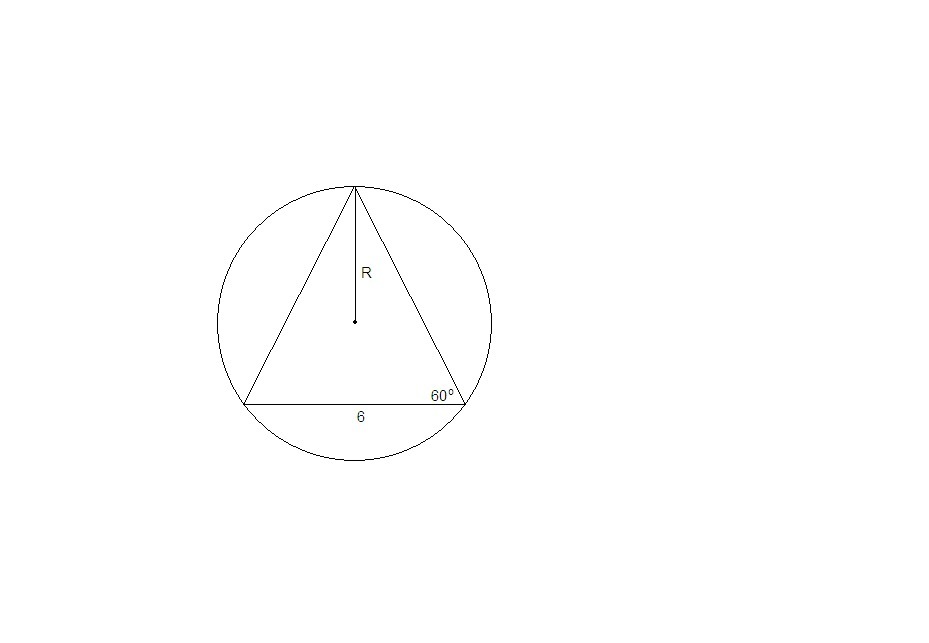
Рассмотрим осевое сечение конуса. Так как центр описанного шара лежит на высоте конуса, сечение проходит через центр шара.
Имеем равнобедренный треугольник и описанную около него окружность, радиус которой равен радиусу шара.
Угол наклона образующей к основанию 60°, значит треугольник равносторонний со стороной 6 см.
Радиус окружности, описанной около равностороннего треугольника со стороной а, равен
R = a√3/3
R = 6√3/3 = 2√3 см
Vшара = 4/3 πR³ = 4/3 π · 2³ · 3√3 = 32π√3 см³