Предмет: Алгебра, автор: Diefriday

Нужно решить только под б, в и д

Приложения:

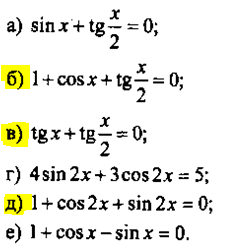
Ответы

Автор ответа: m11m

б)
$1+cosx+tg frac{x}{2} =0 \ \ 1+ frac{1-tg^2( frac{x}{2} )}{1+tg^2( frac{x}{2} )}+tg( frac{x}{2} )=0 \ \ x neq pi+2 pi n \ \$
$1+ frac{1-y^2}{1+y^2}+y=0 \ \ 1+y^2+1-y^2+y(1+y^2)=0 \ 2+y+y^3=0 \ y^3+y+2=0$

При у= -1 (-1)³ -1+2=-1-1+2=0
у= -1 - корень уравнения.

у³+у+2=(у+1)(у² -у+2)

(у+1)(y² -y+2)=0
a) y+1=0 b) y² -y+2=0
y= -1 D=1-8= -7<0
нет решений.

$tg( frac{x}{2} )= -1 \ \ frac{x}{2}=- frac{ pi }{4}+ pi n \ \ x= - frac{ pi }{2}+2 pi n$ , n∈Z

Ответ: $- frac{ pi }{2}+2 pi n,$ n∈Z.

в)
$tgx+tg frac{x}{2}=0 \ \ frac{2tg frac{x}{2} }{1-tg^2( frac{x}{2} )}+tg frac{x}{2} =0 \ \ x neq pi +2 pi n \ \ \ y=tg frac{x}{2}$

$frac{2y}{1-y^2}+y=0 \ \ 2y+y(1-y^2) =0 \ 2y+y-y^3=0 \ y^3-3y=0 \ y(y^2-3)=0 \ \ 1) y=0 \ \ 2) y^2-3=0 \ y^2=3 \ y_{1}= sqrt{3} \ y_{2}=- sqrt{3}$

При у=0
$tg frac{x}{2}=0 \ frac{x}{2}= pi n \ \ x=2 pi n$

При у=(+/-)√3
$frac{x}{2}=(+/-) frac{ pi }{3}+ pi n \ \ x=(+/-) frac{2 pi }{3}+2 pi n$ , n∈Z

Ответ: $(+/-) frac{2 pi }{3}+2 pi n,$ n∈Z;
$2 pi n, n$ ∈Z.

д) 1+cos2x+sin2x=0
1+cos²x-sin²x+2sinxcosx=0
cos²x+sin²x+cos²x-sin²x+2sinxcosx=0
2cos²x+2sinxcosx=0
cos²x+sinxcosx=0
cosx(cosx+sinx)=0

a) cosx=0
$x= frac{x}{2}+ pi n$ , n∈Z.

б) cosx+sinx=0
$cosx+cos( frac{ pi }{2}-x )=0 \ \ 2cos frac{x+ frac{ pi }{2}-x }{2}cos frac{x-( frac{ pi }{2} -x)}{2}=0 \ \ 2cos frac{ pi }{4}cos frac{2x- frac{ pi }{2} }{2}=0 \ \ 2* frac{ sqrt{2} }{2}*cos frac{4x- pi }{4}=0 \ \ cos frac{4x- pi }{4}=0 \ \ frac{4x- pi }{4}= frac{ pi }{2}+ pi n \ \ 4x- pi =2 pi +4 pi n \ 4x=2 pi + pi +4 pi n \ 4x=3 pi +4 pi n \ x= frac{3 pi }{4}+ pi n$ , n∈Z

Ответ: $frac{ pi }{2}+ pi n$ , n∈Z;
$frac{3 pi }{4}+ pi n$ , n∈Z.