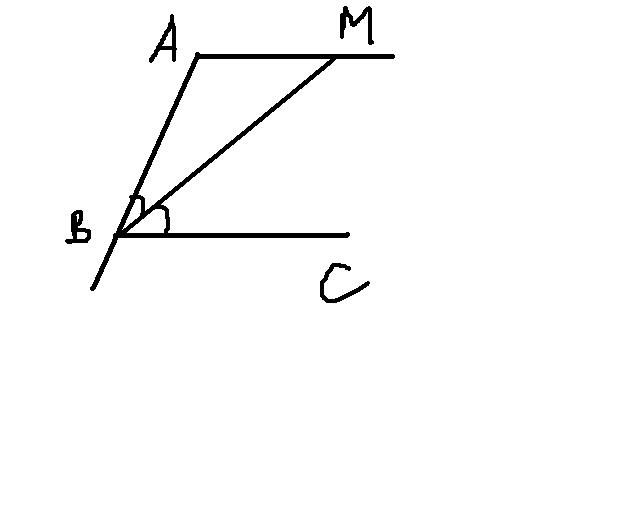
Дан треугольник АВС,равный 75 градусам.Через точку А проведена прямая,параллельная прямой ВС и пересекающая биссектрису угла в точке М.Найдите углы треугольника АВМ.

Сначала для удобства отмечу на прямой АМ точку Р, лежащую по другую сторону от А.
 угАВМ =угВ/2=37,5
угАВР=угВ=75(т к они накрест леж. при параллельных АМ и ВС)
уг ВАМ=180-угАВМ=105(т к эти углы смежны)
По теореме о сумме углов
угМ=180-угАВМ-угВАМ=37,5
Ответ: 37,5; 105; 37,5 

угол ABM = 75/2 = 37.5 гр. (BM бисс)

угол CBO = 180-75 = 105 (смежные углы)

угол MAB = углу CBO = 105 гр.  (соответсвеные углы при AM||BC сек AB)

 угол AMB = 180-105-37.5 = 37.5 гр.

углы тр-ка ABM равны 105, 37,5 и 37,5

или

угол ABM = углу MBC = 75/2 = 37.5 гр. (BM бисс)

угол MBC = углу BMA = 37.5 (накрест лежащие при AM||BC сек AB)

угол BAM = 180-37.5-37.5 = 105 гр.