Предмет: Геометрия,
автор: Ifowolf
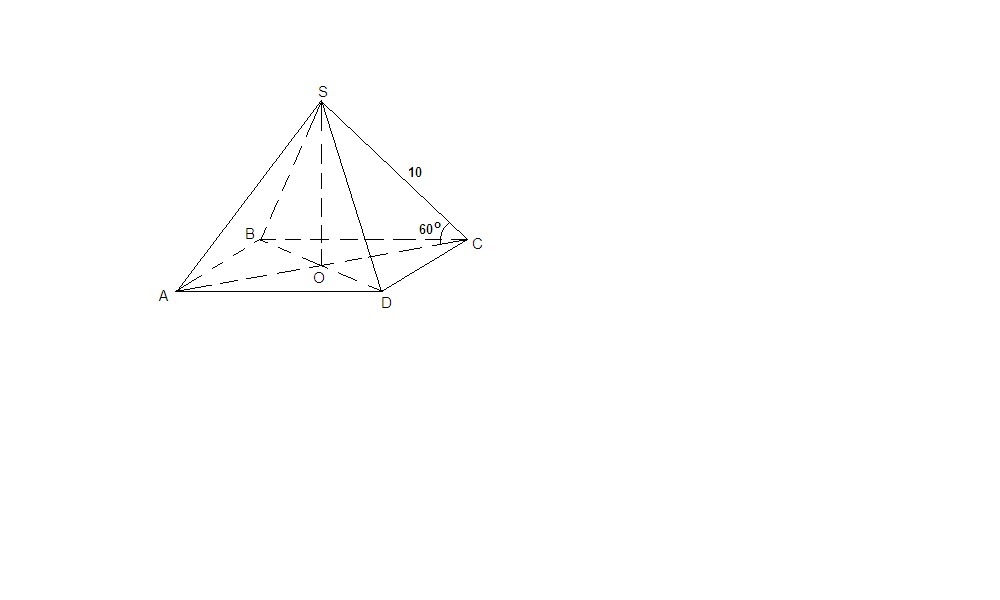
В правильной четырехугольной пирамиде боковые ребра наклонены к основанию под углом 60 градусов. Длина бокового ребра равна 10 см. Найти объем пирамиды.
Ответы
Автор ответа:
0
Пирамида правильная, значит в основании квадрат, все боковые ребра равны и высота проецируется в центр основания.
ΔASC - равнобедренный (SA = SC = 10 см) с углом 60° при основании, значит равносторонний,
АС = SA = 10 см.
SO - высота пирамиды и высота равностороннего треугольника:
SO = AC√3/2 = 10√3/2 = 5√3 см
Площадь квадрата равна половине произведения его диагоналей (как у любого ромба), а диагонали у него равны:
Sabcd = AC²/2 = 100/2 = 50 см²
Объем пирамиды:
V = 1/3 · Sabcd · SO = 1/3 · 50 · 5√3 = 250√3/3 см³
Приложения:
Интересные вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Другие предметы,
автор: DSA45689
Предмет: История,
автор: perevalovakata
Предмет: История,
автор: marsik96
Предмет: Химия,
автор: T1mka97