Помогите решить!!! Сторона правильного треугольника вписанного в окружность равна 5корней из 3 см Найдите сторону правильного шестиугольника описанного около этой окружности?

Радиус окружности, описанной около правильного треугольника:
R = a√3/3, где а - сторона правильного треугольника.
R = 5√3·√3/3 = 5 см

Эта же окружность - вписанная в правильный шестиугольник.
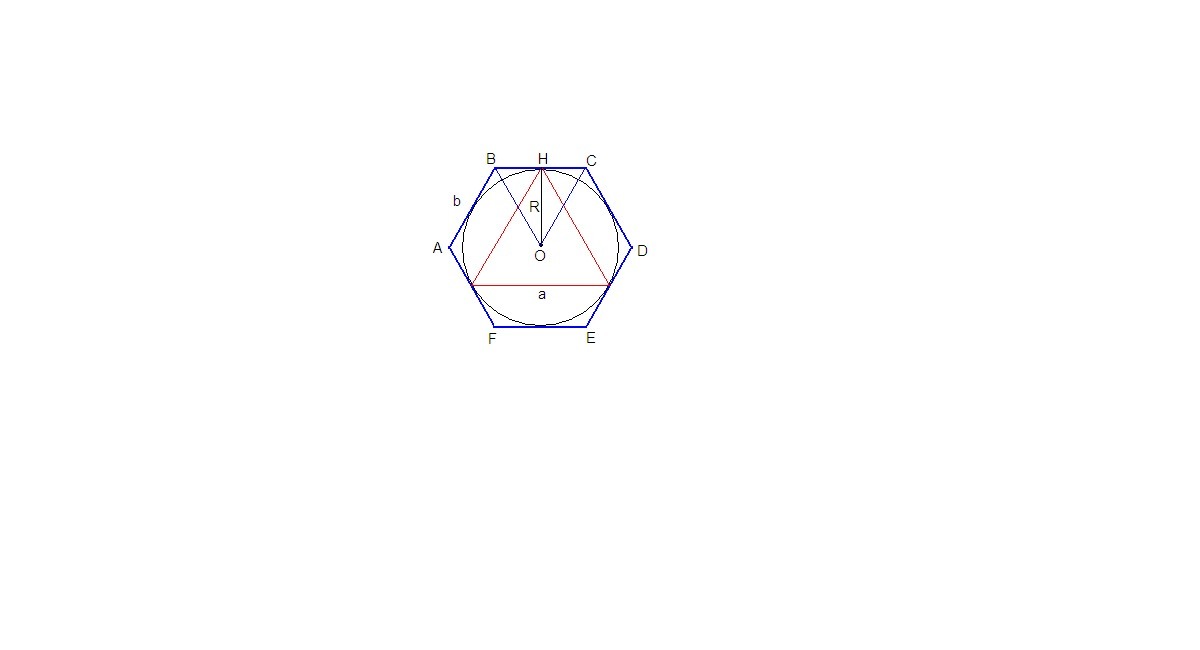
R = OH  - радиус окружности, вписанной в правильный шестиугольник.
ΔВОС равносторонний (ОВ = ОС как радиусы и центральный угол ВОС равен 360°/6 = 60°).
ОН - высота равностороннего треугольника.
ОН = b√3/2
5 = b√3/2
b = 5 · 2 / √3 = 10/√3 = 10√3/3 (см)
R = а√3/2
5 = ·√3/2