Предмет: Алгебра,
автор: Florida777
ПОМОГИТЕ!НАЙДИТЕ ИНТЕГРАЛ!
Приложения:
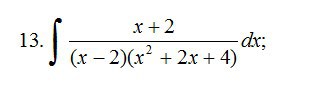
Ответы
Автор ответа:
0
Интересные вопросы
Предмет: Информатика,
автор: Pro007yu
Предмет: Қазақ тiлi,
автор: DeidaraC4
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Аноним
Предмет: Литература,
автор: nikitaprofu42