Предмет: Алгебра, автор: rally8954

Помогите решить интегралы

Приложения:

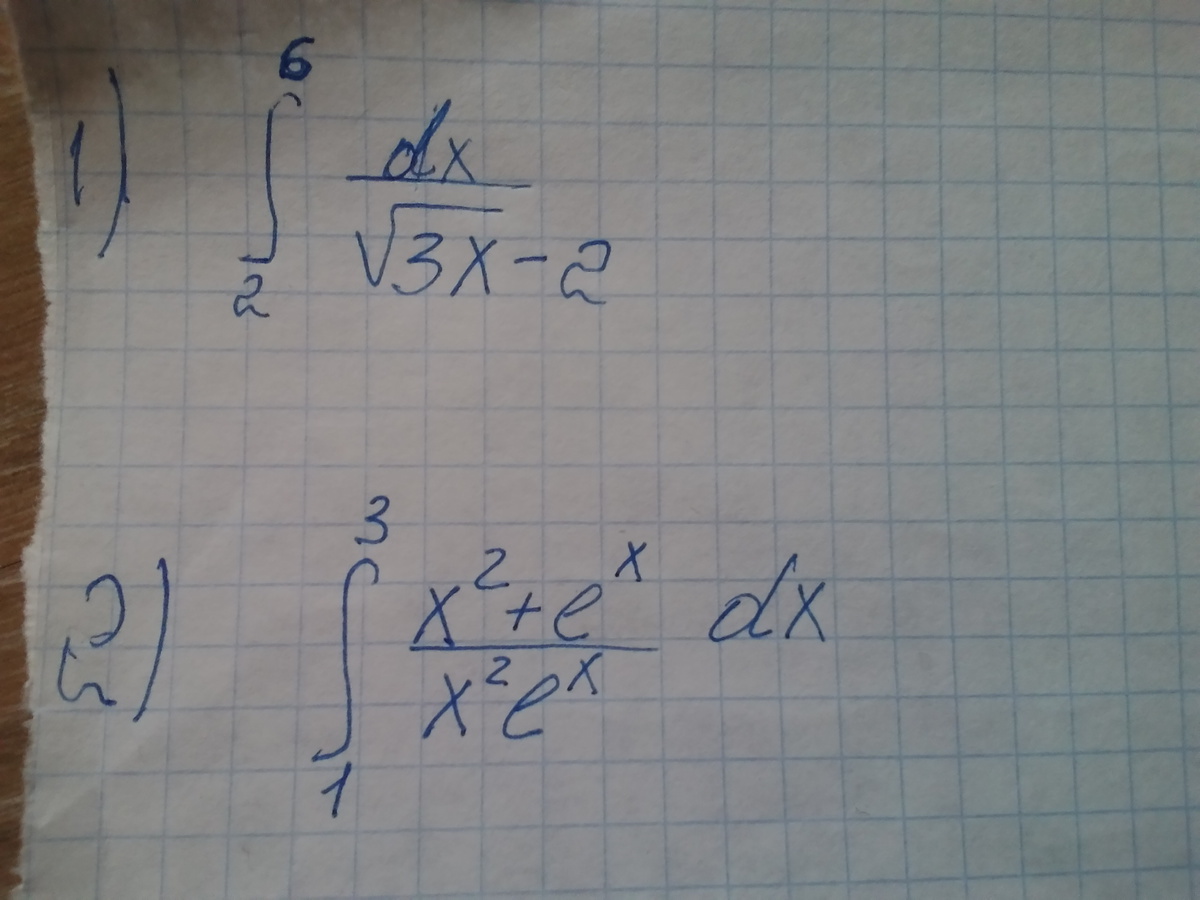
Ответы

Автор ответа: gartenzie

1.

$int{ frac{ dx }{ sqrt{3x} - 2 } } = frac{1}{3} int{ frac{ d ( sqrt{3x} )^2 }{ sqrt{3x} - 2 } } = frac{2}{3} int{ frac{ sqrt{3x} d sqrt{3x} }{ sqrt{3x} - 2 } } = frac{2}{3} int{ frac{ sqrt{3x} - 2 + 2 }{ sqrt{3x} - 2 } } , d sqrt{3x} = \\ = frac{2}{3} int{ ( frac{ sqrt{3x} - 2 }{ sqrt{3x} - 2 } + frac{2}{ sqrt{3x} - 2 } ) } , d sqrt{3x} = frac{2}{3} int{ ( 1 + frac{2}{ sqrt{3x} - 2 } ) } , d sqrt{3x} = \\ = frac{2}{3} int{ d sqrt{3x} } + frac{4}{3} int{ frac{ d ( sqrt{3x} - 2 ) }{ sqrt{3x} - 2 } } = frac{2}{3} sqrt{3x} + frac{4}{3} ln{ | sqrt{3x} - 2 | } + C ;$

$intlimits_2^6{ frac{ dx }{ sqrt{3x} - 2 } } = frac{2}{3} sqrt{3x} |_2^6 + frac{4}{3} ln{ | sqrt{3x} - 2 | } |_2^6 = \\ = frac{2}{3} ( sqrt{ 3 cdot 6 } - sqrt{ 3 cdot 2 } ) + frac{4}{3} ( ln{ | sqrt{ 3 cdot 6 } - 2 | } - ln{ | sqrt{ 3 cdot 2 } - 2 | } ) = \\ = frac{2}{3} ( 3 sqrt{2} - sqrt{ 3 cdot 2 } ) + frac{4}{3} ln{ frac{ 3 sqrt{2} - 2 }{ sqrt{ 3 cdot 2 } - 2 } } = frac{ 2 sqrt{2} }{ sqrt{3} } ( sqrt{3} - 1 ) + frac{4}{3} ln{ frac{ ( 3 sqrt{2} - 2 ) ( sqrt{ 3 cdot 2 } + 2 ) }{ ( sqrt{ 3 cdot 2 } - 2 ) ( sqrt{ 3 cdot 2 } + 2 ) } } = \\ = 2 sqrt{ frac{2}{3} } ( sqrt{3} - 1 ) + frac{4}{3} ln{ frac{ ( 6 sqrt{3} - 2 sqrt{ 3 cdot 2 } + 2 sqrt{ 3 cdot 2 } - 4 ) }{ ( ( sqrt{ 3 cdot 2 } )^2 - 2^2 ) } } = \\ = 2 sqrt{ frac{2}{3} } ( sqrt{3} - 1 ) + frac{4}{3} ln{ frac{ ( 6 sqrt{3} - 4 ) }{ ( 6 - 4 ) } } ;$

$intlimits_2^6{ frac{ dx }{ sqrt{3x} - 2 } } = 2 sqrt{2} ( 1 - frac{1}{ sqrt{3} } ) + frac{4}{3} ln{ ( 3 sqrt{3} - 2 ) } .$

2.

$int{ frac{ x^2 + e^x }{ x^2 e^x } } , dx = int{ ( frac{ x^2 }{ x^2 e^x } + frac{ e^x }{ x^2 e^x } ) } , dx = int{ ( frac{1}{e^x} + frac{1}{x^2} ) } , dx = \\ = int{ e^{-x} } , dx + int{ x^{-2} } , dx = C - e^{-x} - frac{1}{x} ;$

$intlimits_1^3 { frac{ x^2 + e^x }{ x^2 e^x } } , dx = e^{-x} |^1_3 + frac{1}{x} |^1_3 = frac{1}{e} - frac{1}{e^3} + 1 - frac{1}{3} ;$

$intlimits_1^3 { frac{ x^2 + e^x }{ x^2 e^x } } , dx = frac{1}{3} + frac{1}{e} ( 1 - frac{1}{e^2} ) .$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Химия, автор: greskoandrii2

срочно дам 50 балов за правильное!!!!!! що значать такі записи Ar(ca). , Mr(Co). ,w{S}

6 лет назад

Предмет: История, автор: kristinabykova350

Прошу, помогите - Краткое содержание по парагрофу 18 история россии 7 класс Данилов (помогите пож)

6 лет назад

Предмет: География, автор: Аноним

Прведите пример осадочных горных пород различного происхождения 1) обломочные2) химические 3) органические

6 лет назад

Предмет: Алгебра, автор: Misaki14

верно ли равенство 4/21 <3/17,5/8<8/13

9 лет назад

Предмет: Математика, автор: mekan1

отправляясь гулять мряка каждый раз надевает 3фуфыры а бряка только2 домой они обе всегда возращаются совершенно голые сколько фуфыр растеряли мряка и бряка за лето если известно что мряка гуляла летом 150 раз а бряка 180 раз

9 лет назад