Предмет: Математика,
автор: 1898ш
решите неравенство: пооооомогитее 56-58 Б
Приложения:
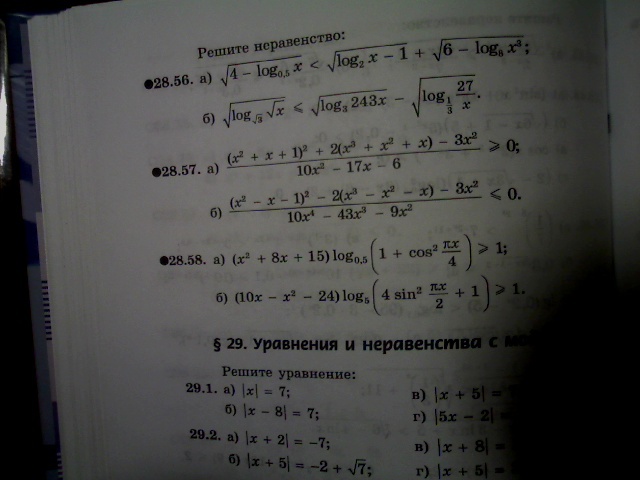
Ответы
Автор ответа:
0
Делаем по действиям. Приводим все логарифмы к основанию 3.
1)
2)
3)
Подставляем
Область определения
Замена
√y <= √(y+5) - √(y-3)
√y + √(y-3) <= √(y+5)
Возводим в квадрат
y + 2√(y(y-3)) + y-3 <= y+5
Оставляем корень слева, остальное переносим вправо
2√(y^2 - 3y) <= y+5-y-y+3
2√(y^2 - 3y) <= 8 - y
√(y^2 - 3y) <= (8 - y)/2
Снова возводим в квадрат
y^2 - 3y <= (y^2 - 16y + 64)/4
4y^2 - 12y <= y^2 - 16y + 64
3y^2 + 4y - 64 <= 0
D/4 = 2^2 - 3(-64) = 4 + 192 = 196 = 14^2
y1 = (-2 - 14)/3 = -16/3 < 3
y2 = (-2 + 14)/3 = 12/3 = 4
y ∈ [3; 4]
Обратная замена
x ∈ [27; 81]
Автор ответа:
0
58 можно решить точно также, а 57 - дробь < 0, когда числитель и знаменатель имеют разные знаки. Но все это писать в одном вопросе - слишком объемно.
Интересные вопросы
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Аноним
Предмет: Английский язык,
автор: yveliev
Предмет: Математика,
автор: rekrut78
Предмет: Математика,
автор: atyatankaroman