Предмет: Алгебра, автор: sashavolk

Решить системы уравнений

Приложения:

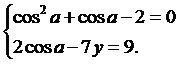
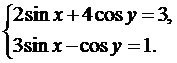
Ответы

Автор ответа: mukus13

$1)$

$left { {{cos^2 alpha +cos alpha -2=0} atop {2cos alpha -7y=9}} right.$

Решим отдельно первое уравнение системы:

$cos^2 alpha +cos alpha -2=0$

Замена: $cos alpha =t,$ $| t| leq 1$

$t^2+t-2=0$

$D=1^2-4*1*(-2)=1+8=9$

$t_1= frac{-1+3}{2} =1$

$t_2= frac{-1-3}{2} =-2$ - не подходит

Вернемся к системе уравнений:

$left { {{cos alpha =1} atop {2cos alpha -7y=9}} right.$

$left { {{cos alpha =1} atop {2*1 -7y=9}} right.$

$left { {{cos alpha =1} atop { -7y=7}} right.$

$left { {{ alpha =2 pi n, } atop { y=-1}} right.$

Ответ: $( 2 pi n,$ $n$ ∈ $Z;-1)$

$2)$

$left { {{2sinx+4cosy=3} atop {3sinx-cosy=1}} right.$

$left { {{2sinx+4cosy=3} atop {12sinx-4cosy=4}} right.$

$left { {{14sinx=7} atop {2sinx+4cosy=3}} right.$

$left { {{sinx= frac{1}{2} } atop {2sinx+4cosy=3}} right.$

$left { {{sinx= frac{1}{2} } atop {2* frac{1}{2} +4cosy=3}} right.$

$left { {{sinx= frac{1}{2} } atop {1 +4cosy=3}} right.$

$left { {{sinx= frac{1}{2} } atop {4cosy=2}} right.$

$left { {{sinx= frac{1}{2} } atop {cosy= frac{1}{2} }} right.$

$left { {{x= (-1)^k arcsinfrac{1}{2}+ pi k } atop {y=(+/-) arccos frac{1}{2}+2 pi n }} right.$

$left { {{x= (-1)^k frac{ pi }{6} + pi k } atop {y=(+/-) frac{ pi }{3} +2 pi n }} right.$

Ответ: $( (-1)^k frac{ pi }{6} + pi k,$ $k$ ∈ $Z;$ ± $frac{ pi }{3} +2 pi n,$ $n$ ∈ $Z)$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Математика, автор: L0lit0chka

Помогите с 1200 и 1205

6 лет назад

Предмет: Информатика, автор: Аноним

с++
Cамый дешёвый путь
В каждой клетке прямоугольной таблицы N×M записано некоторое число. Изначально игрок находится в левой верхней клетке. За один ход ему разрешается перемещаться в соседнюю клетку либо вправо, либо вниз (влево и вверх перемещаться запрещено). При проходе через клетку с игрока берут столько килограммов еды, какое число записано в этой клетке (еду берут также за первую и последнюю клетки его пути).

Требуется найти минимальный вес еды в килограммах, отдав которую игрок может попасть в правый нижний угол.

Входные данные

Вводятся два числа N и M — размеры таблицы 1≤N≤20,1≤M≤20. Затем идёт N строк по M чисел в каждой — размеры штрафов в килограммах за прохождение через соответствующие клетки (числа от 0 до 100).

Выходные данные

Выведите минимальный вес еды в килограммах, отдав которую можно попасть в правый нижний угол.

Примеры
Ввод
Вывод
5 5
1 1 1 1 1
3 9 9 9 9
1 1 1 1 1
2 2 2 2 1
1 1 1 1 1
11

6 лет назад

Предмет: Другие предметы, автор: 2030149381

Какие три словосочетания- словом "mater"и предшествующим ему а прилагательным Вы знаете?

6 лет назад

Предмет: История, автор: Zabors02

Главное занятие жителей междуречье - .......

9 лет назад

Предмет: Математика, автор: ghgjgktkt

6) Впервый раз мастер получил тридцать три целых одну третью процента оплаты. выполненную работу, во второй раз 2/3 оплаты. какой процент оплаты за всю работу осталось ему получить?

9 лет назад