Предмет: Алгебра,
автор: positive96
помогите решить 1860
Приложения:
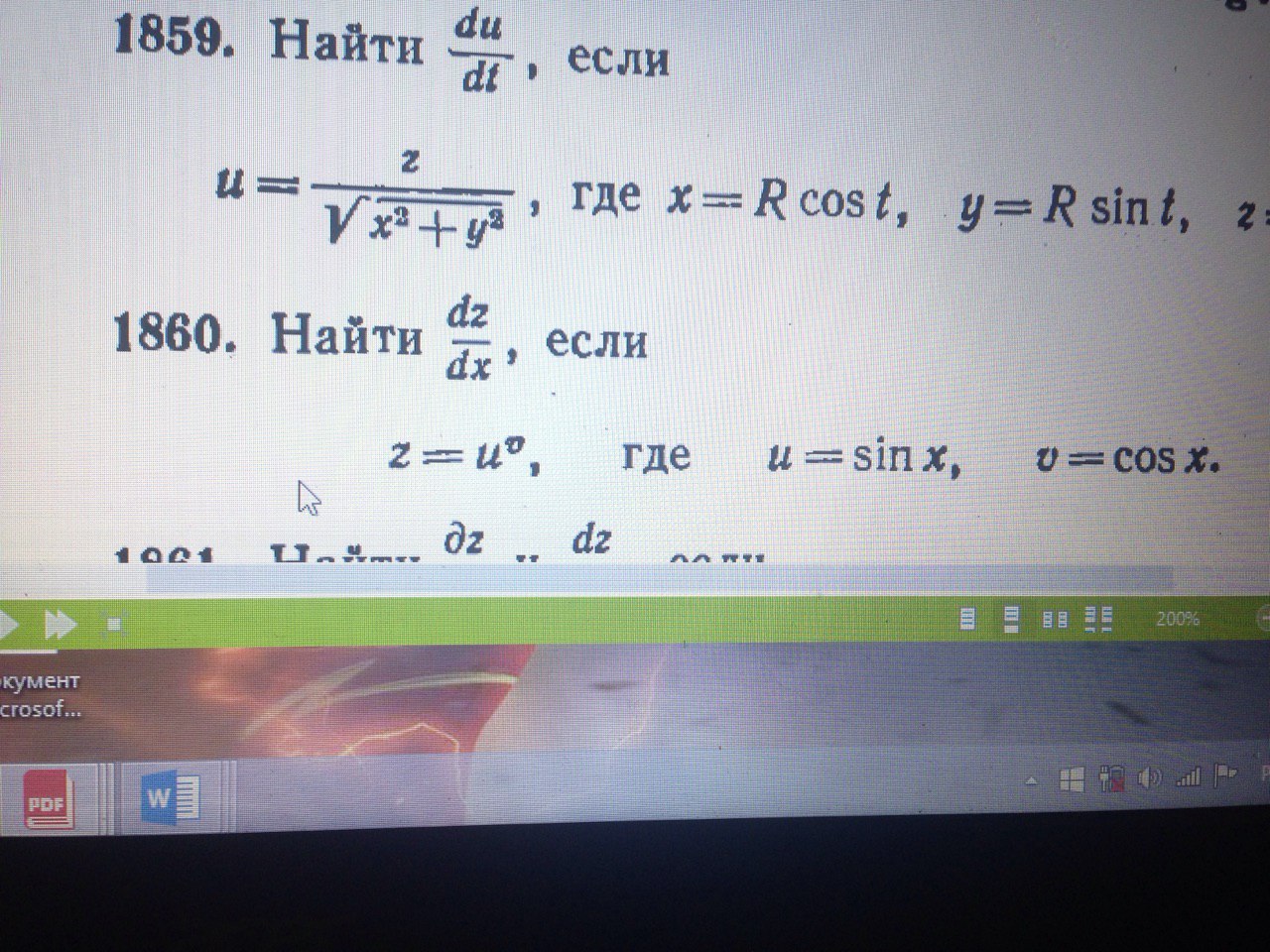
Ответы
Автор ответа:
0
z = u^v; u = sin x; v = cos x
dz/dx = (dz/du)*(du/dx) + (dz/dv)*(dv/dx)
Находим каждую производную отдельно
dz/du=v*u^(v-1)=cos x*(sin x)^(cos x - 1)=cos x/sin x*(sin x)^(cos x)=ctg x*(sin x)^(cos x)
dz/dv = v^y*ln |u| = (sin x)^(cos x)*ln |sin x|
du/dx = cos x
dv/dx = -sin x
Подставляем
dz/dx = (sin x)^(cos x)*(ctg x*cos x - ln |sin x|*sin x)
dz/dx = (dz/du)*(du/dx) + (dz/dv)*(dv/dx)
Находим каждую производную отдельно
dz/du=v*u^(v-1)=cos x*(sin x)^(cos x - 1)=cos x/sin x*(sin x)^(cos x)=ctg x*(sin x)^(cos x)
dz/dv = v^y*ln |u| = (sin x)^(cos x)*ln |sin x|
du/dx = cos x
dv/dx = -sin x
Подставляем
dz/dx = (sin x)^(cos x)*(ctg x*cos x - ln |sin x|*sin x)
Интересные вопросы
Предмет: Українська мова,
автор: artemfootdall
Предмет: Химия,
автор: gundirova67
Предмет: Химия,
автор: sasoklol455
Предмет: Химия,
автор: avp2009
Предмет: Алгебра,
автор: miki000