Предмет: Алгебра,
автор: g2590757
Используя метод математической индукции, докажите, что
Приложения:
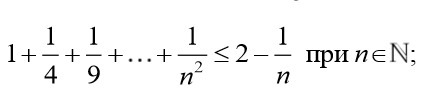
Ответы
Автор ответа:
0
-----------------------------------------------------------------
(РЕШЕНИЕ)
База индукции
При утверждение верно.
утверждение верно. 
Гипотеза индукции. Пусть утверждение верно при
т.е. справедливо неравенство

Индукционный переход
Докажем что тогда справедливо неравенство при
т.е. что тогда справедливо неравенство

или используя предположение нужно доказать что

или

или
что


так как обе части неотрицательны, то равносильно



что очевидно верно
таким образом на основании принципа мат. индукции неравенство доказано.
----------------
(более логичное решение)
неравенство равносильно неравенству

заметим что при n є N,

поєтому




т.е. нужно получили требуемое
(РЕШЕНИЕ)
База индукции
При
Гипотеза индукции. Пусть утверждение верно при
т.е. справедливо неравенство
Индукционный переход
Докажем что тогда справедливо неравенство при
т.е. что тогда справедливо неравенство
или используя предположение нужно доказать что
или
или
что
так как обе части неотрицательны, то равносильно
что очевидно верно
таким образом на основании принципа мат. индукции неравенство доказано.
----------------
(более логичное решение)
неравенство равносильно неравенству
заметим что при n є N,
поєтому
т.е. нужно получили требуемое
Интересные вопросы
Предмет: Математика,
автор: sveta19977778
Предмет: Математика,
автор: katamalina714
Предмет: Английский язык,
автор: sergeygri2002
Предмет: Математика,
автор: taka86
Предмет: Химия,
автор: sultanabdullayev