Предмет: Математика, автор: oleg70rus

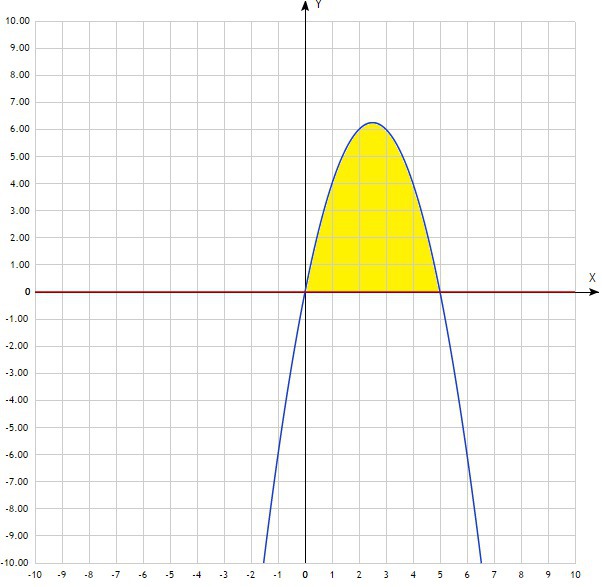
вычислить площадь фигуры, ограниченной линиями
y=-x²+5x и y=0

Ответы

Автор ответа: Utem

0

Чертим чертёж. Находим пределы интегрирования
-x²+5x=0
x(5-x)=0
x=0 x=5
Искомая фигура ограничена сверху параболой ветви, которой направлены вниз, и осью ОХ (у=0).
Находим площадь с помощью определённого интеграла
$s= intlimits^5_0 {(-x^2+5x)} , dx =(- frac{x^3}{3}+ frac{5x^2}{2})|_0^5=- frac{5^3}{3}+ frac{5*5^2}{2}= frac{125}{3}=20 frac{5}{6}$ ед²

Приложения:

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Биология, автор: kendtik2334

3. Відповіддю на подразнення за участю
нервової системи є
А таксис.
Б рефлекс.
В тропізм.
Г настія.

4. За допомогою якої речовини передається
збудження у синапсі?
А мієліну
Б ферменту
В нейромедіатора
Г фосфоліпіду

6 лет назад

Предмет: Химия, автор: clashgamesakk01

Наземная концентрации вещества А в системе А + В=С 0.22 моль через 10с она стала 0.215 моль.Вычеслите скорость скорость химической реакции. СРОЧНО НАДО!!!

6 лет назад

Предмет: Экономика, автор: nastyayureva290

Сопоставьте экономическое развитие России и Германии во второй половине
ХIХв.

6 лет назад

Предмет: Математика, автор: arpine198707

ЧАСТНОЕ ЧИСЕЛ 21 И 7ТУВЕЛИЧИТЬ В 9 РАЗ .ПРОИЗВЕДЕНИЕ ЧИСЕЛ 6 И 3 УМЕНЬШИТЬ В 2 РАЗА.ПРОИЗВЕДЕНИЕ ЧИСЕЛ 4 И 4 УМЕНЬШИТЬ В 8 РАЗ.ЧАСТНОЕ ЧИСЕЛ 72 И 8 УВЕЛИЧИТЬ В 9 РАЗ

9 лет назад

Предмет: Химия, автор: Bazuka02

В каком ряду находится вещества только с ковалентной связью - назвать выбранные вещества, указать полярная или неполярная связь:

A) F2, Fe, HCl
Б) N2, HCI, P2O5
В) NaCl, CaO, K3PO4

9 лет назад