Предмет: Алгебра,
автор: Аноним
Какому числу при всех допустимых значениях а равно значение выражения:

Ответы
Автор ответа:
0
Решение на фото!!!!!!!!!!!!!!!!!!!!!!!!!!
Приложения:
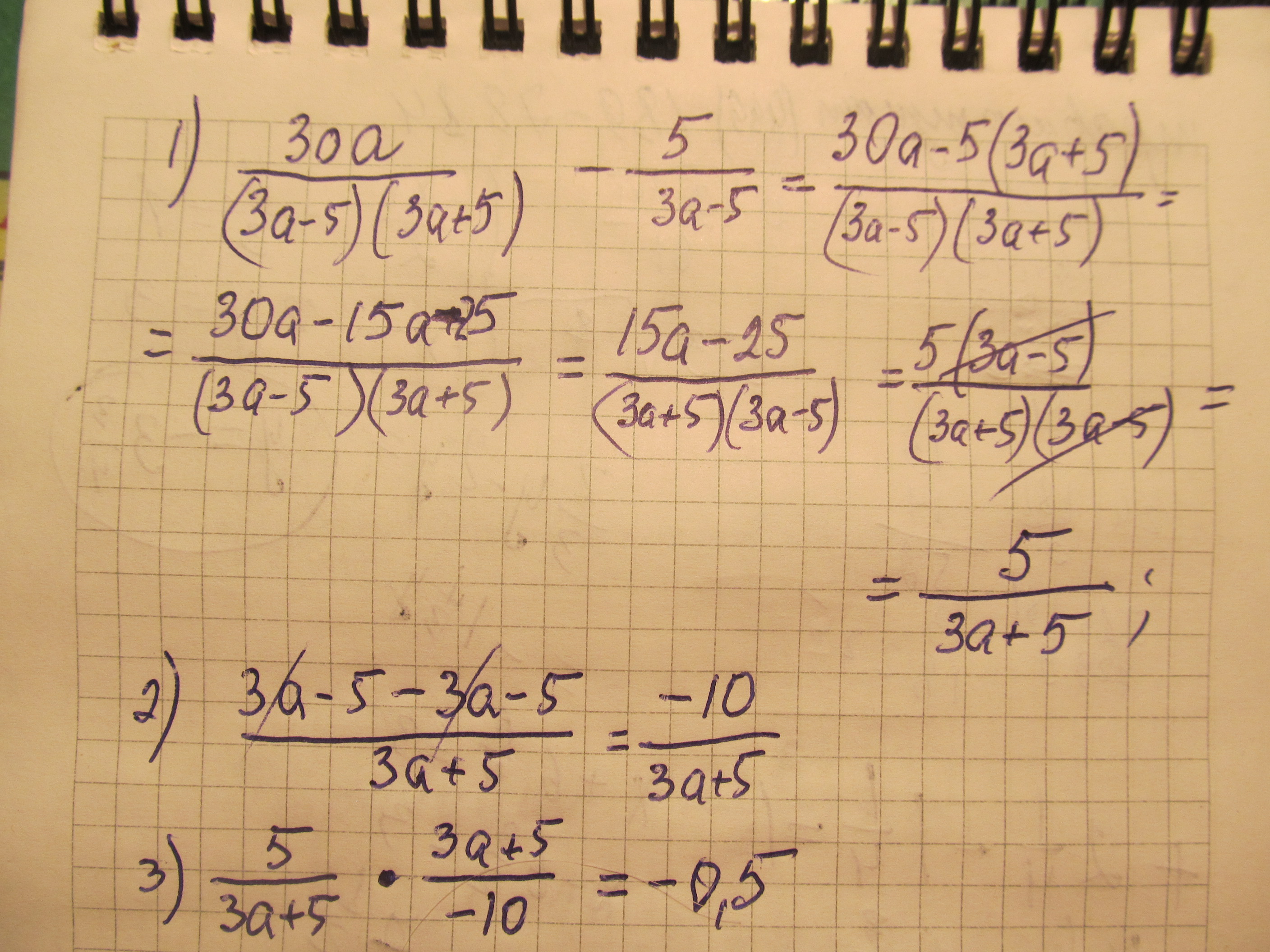
Автор ответа:
0
Все знают с начальной школы, что
Очередные свойства алгебраической дроби. Ведь
Осталось выполнить деление дробей и найти ответ.
Ответ: значение выражения
Приложения:
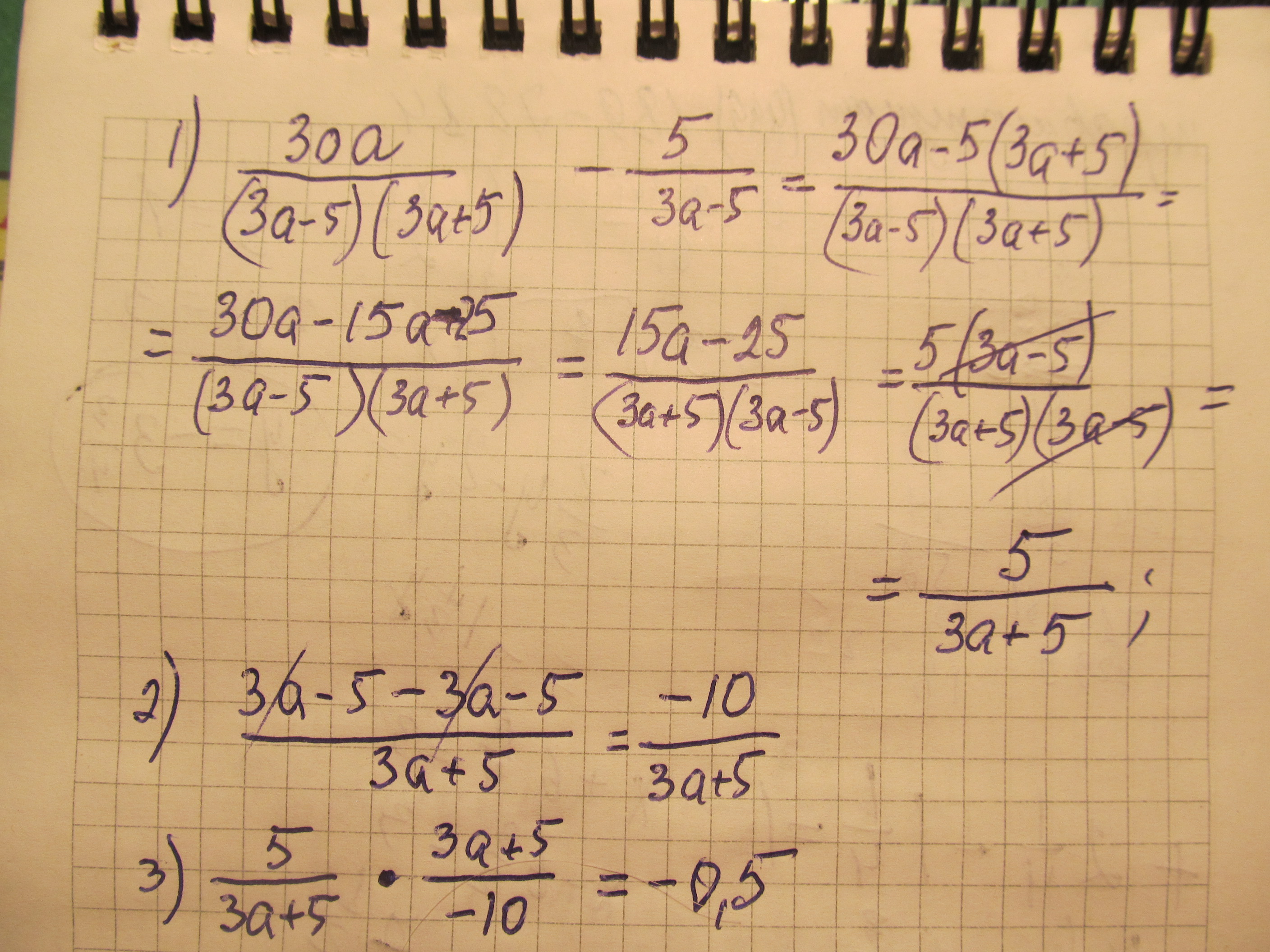
Автор ответа:
0
только не просто 0,5 , а -0,5 :D
Автор ответа:
0
Ой, точно
Автор ответа:
0
:D пасиб
Интересные вопросы
Предмет: Английский язык,
автор: pivenmarser
Предмет: Геометрия,
автор: hassell
Предмет: Биология,
автор: polinakutepova13
Предмет: Математика,
автор: love0ls0
Предмет: Химия,
автор: olya9740