Предмет: Математика,
автор: Игорь996
Найдите сумму целых решений неравенства!
Приложения:
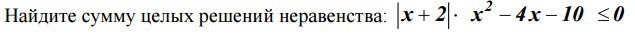
Ответы
Автор ответа:
0
Чисто подбором находим целые решения, так как решать кубические неравенства не очень приятно.
0, ±1, ±2, больше решений нет, так как ф-ция f(x) = |x + 2|x² - 4x - 10 пересекает ось Ох только в двух точках.
Σ = 0 + 1 - 1 + 2 - 2 = 0
Ответ: 0
0, ±1, ±2, больше решений нет, так как ф-ция f(x) = |x + 2|x² - 4x - 10 пересекает ось Ох только в двух точках.
Σ = 0 + 1 - 1 + 2 - 2 = 0
Ответ: 0
Автор ответа:
0
Надо было сразу условие писать верно.
Автор ответа:
0
Этот ответ считается правильным, потому что отвечает вопросу
Автор ответа:
0
okneret, Напишите в ответах как у вас получилось 14?
Автор ответа:
0
Если скобки поставить и разложить трехчлен на множители, то выйдет это: |х + 2|(х - 2 - √14)(х - 2 + √14) ≤ 0. Дальше раскрываем модуль привычным способом и получаем решение методом интервалов: х ∈ [2 - √14; 2 + √14]. В этот промежуток входят только такие целые числа: 0, ±1, 2, 3, 4 и 5. Тогда Σ = 2 + 3 + 4 + 5 = 14
Автор ответа:
0
Ix+2l>=0 при любых х, тогда х^2-4х-10 <=0. Находим корни с помощью дискриминанта и применяем метод интервалов. Дальше смотри у gflrsov
Интересные вопросы
Предмет: Английский язык,
автор: alena4668
Предмет: Биология,
автор: Leastsq
Предмет: Математика,
автор: olegsolodikhin4
Предмет: Математика,
автор: zeinab0526