Предмет: Алгебра, автор: goscha463727

Решите примеры пожалуйста, полностью, даю 32 балла))

Приложения:

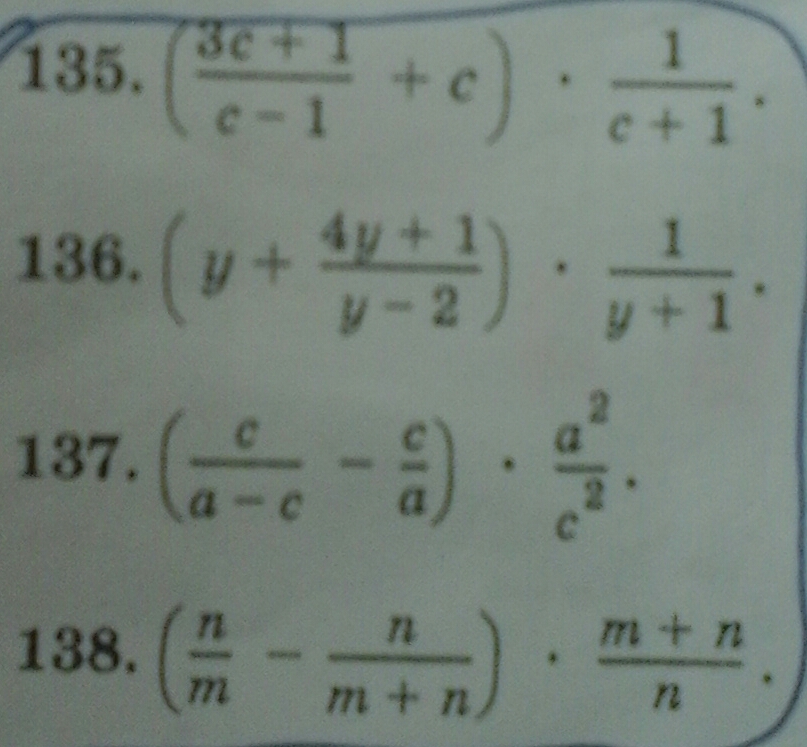
Ответы

Автор ответа: miron2077

!!!!!!!!!!!!!!!!!!!!!!!!!!!

Приложения:

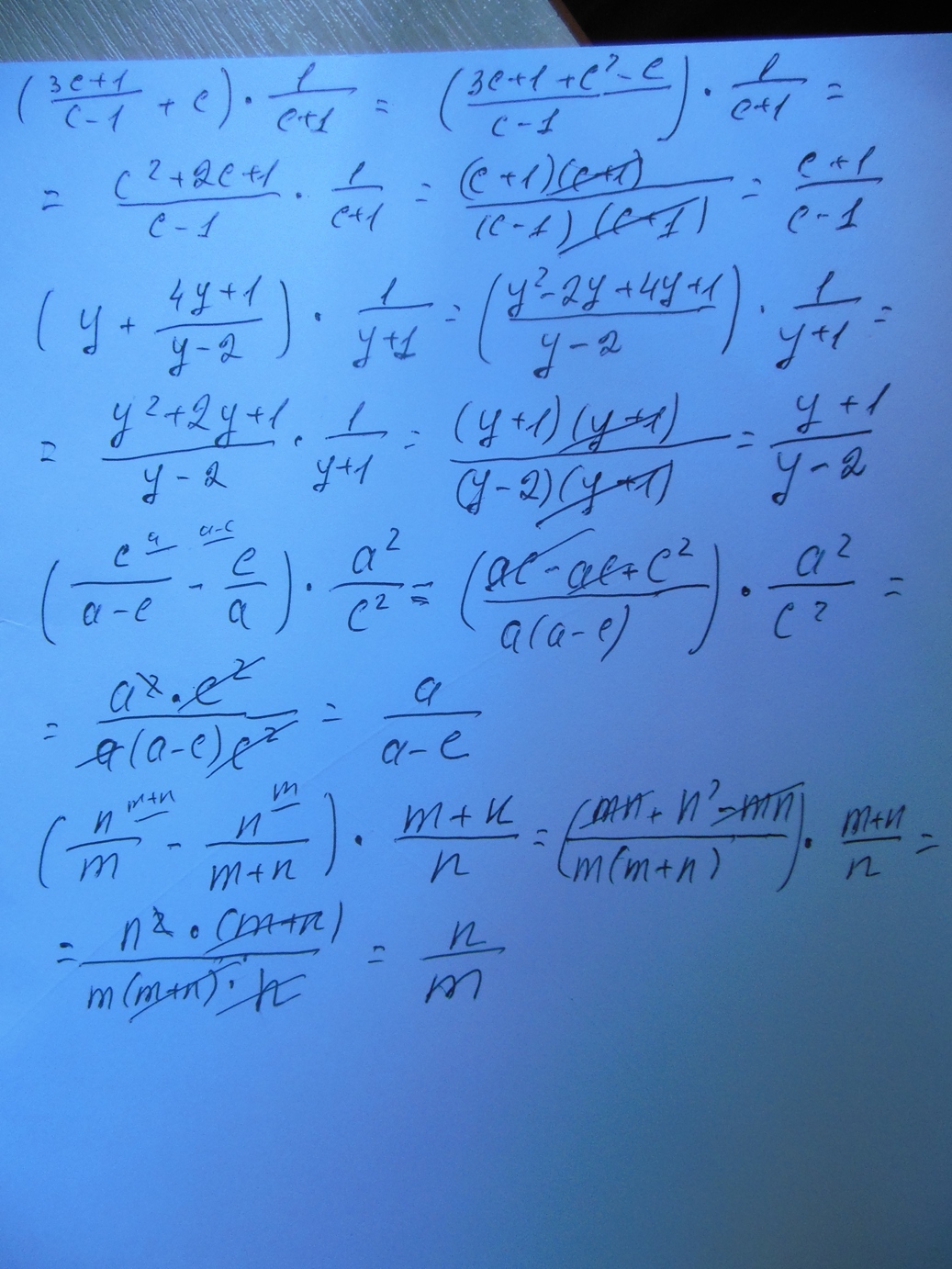
Автор ответа: Alexandr130398

если не отображается решение, то смотри скрин.

$1)( frac{3c+1}{c-1} +c)* frac{1}{c+1} =( frac{3c+1}{c-1} + frac{c(c-1)}{c-1)})* frac{1}{c+1} = frac{3c+1+c^2-c}{c-1} * frac{1}{c+1}= \ \ = frac{c^2+2c+1}{c-1} * frac{1}{c+1}= frac{(c+1)^2}{c-1} * frac{1}{c+1}= frac{c+1}{c-1} \ \ 2)( y+frac{4y+1}{y-2} ) *frac{1}{y+1} = frac{y(y-2)+4y+1}{y-2} *frac{1}{y+1}= frac{y^2-2y+4y+1}{y-2} *frac{1}{y+1}= \ \ =frac{y^2+2y+1}{y-2} *frac{1}{y+1}=frac{(y+1)^2}{y-2} *frac{1}{y+1}= frac{y+1}{y-2}$

$3) ( frac{c}{a-c} - frac{c}{a} )* frac{a^2}{c^2} = frac{ac-c(a-c)}{a(a-c)} * frac{a^2}{c^2}= frac{ac-ac+c^2}{a(a-c)} * frac{a^2}{c^2}= frac{c^2}{a(a-c)}* frac{a^2}{c^2}= \ \ = frac{a}{a-c} \ \ 4) ( frac{n}{m} - frac{n}{m+n} )* frac{m+n}{n} = frac{n(m+n)-mn}{m(m+n)} *frac{m+n}{n} = frac{mn+n^2-mn}{m(m+n)} *frac{m+n}{n} = \ \ = frac{n^2}{m(m+n)} *frac{m+n}{n}= frac{n}{m}$

Приложения: