Помогите! Нужно срочно с подробным решением! Условие в приложении! заранее спасибо!

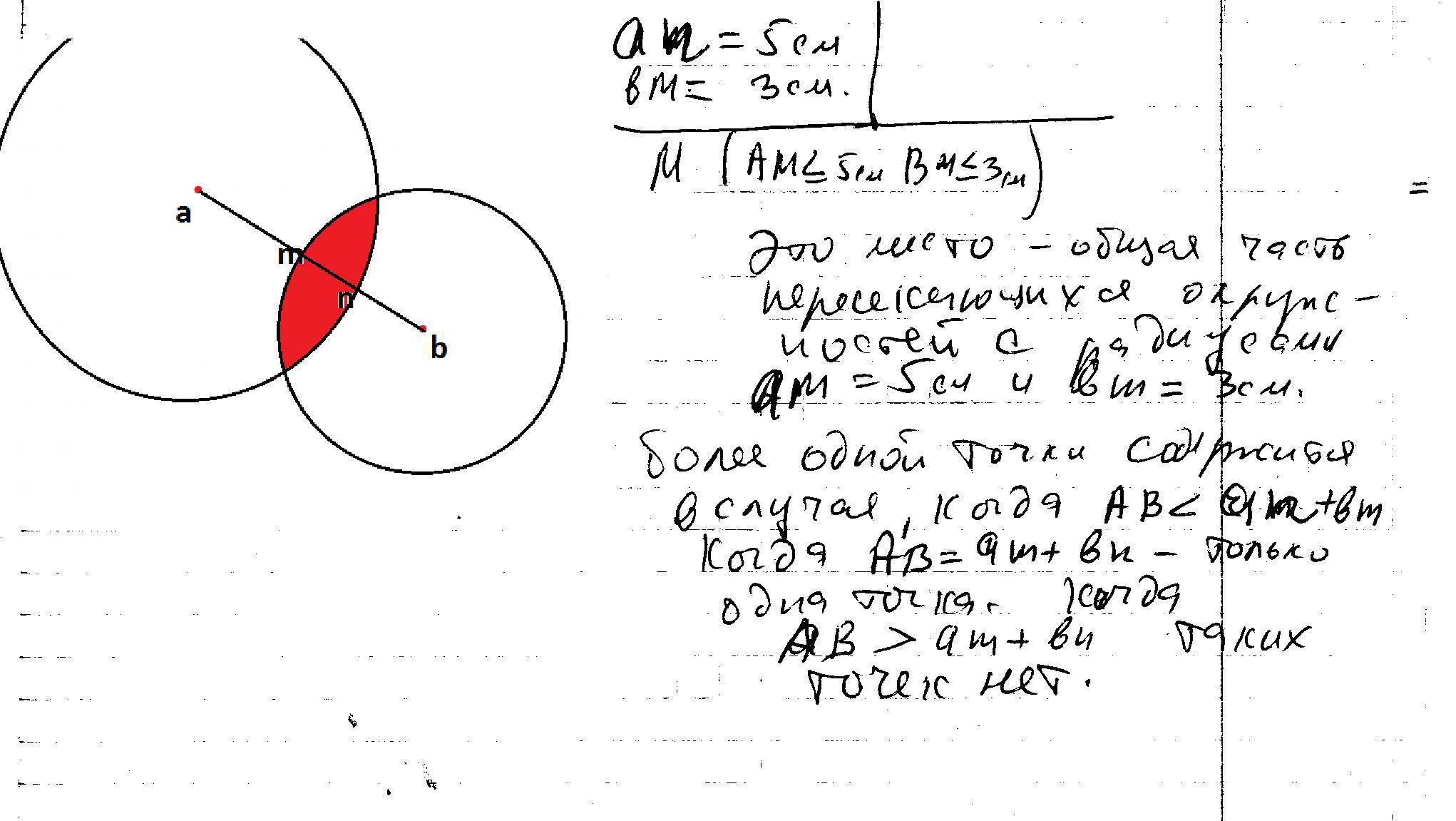
решение в скане.................

Разберем по частям задачу. Геометрическое место точек M, для которых выполняется первое условие, то есть AM <=5, это круг радиуса 5. Аналогично для BM - это круг радиуса 3. Если объединить эти условия, чтобы выполнялось каждое из них, получится пересечение этих кругов. Это пересечение и будет являться искомым геометрическим местом точек M. Возможны несколько случаев взаимного расположения точек A и B. От этого зависит пересечение кругов.
1) Если AB > 8, то пересечения нет.
2) Если AB=8, то пересечением является одна точка M (здесь AM=5, BM=3)
3) Если AB<8, то пересечением будет некоторая общая область этих кругов, содержащая более 1 точки.
Дальнейшие разграничения смысла нет делать, ибо вопрос стоит просто о количестве точек.