в остроугольном треугольнике abc сторона ab равна сторона bc а высота из вершины b 30. на прямой ac взяли точку d так что ad:dc=3:2. найдите радиус окружности, описанной около треугольника bcd

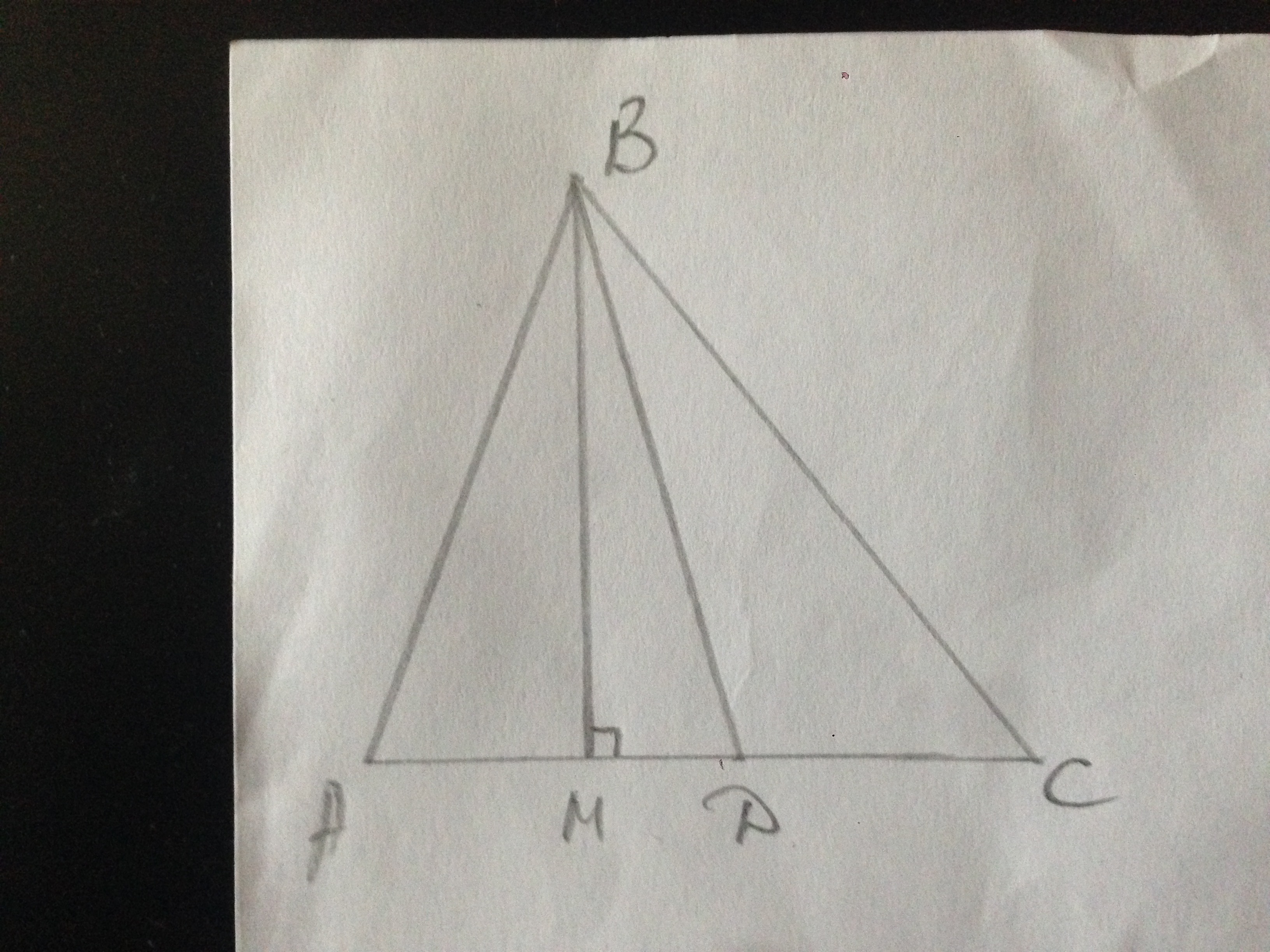
ВМ - высота, ВМ=30.
В прямоугольном тр-ке АВМ АМ=√(АВ²-ВМ²)=√((5√37)²-30²)=5.
В прямоугольном тр-ке СВМ СМ=√(ВС²-ВМ²)=√((10√10)²-30²)=10.
АС=АМ+СМ=5+10=15.
АД:СД=3х:2х ⇒ АС=3х+2х=5х=15 ⇒ х=3.
АД=3х=9, СД=2х=6.
МД=АД-АМ=9-5=4.
В прямоугольном тр-ке ВМД ВД=√(ВМ²+МД²)=√(30²+4²)=√916=2√229.
Площадь тр-ка ВСД: S=CД·ВМ/2=6·30/2=90.
Радиус описанной окружности около тр-ка ВСД:
R=abc/4S=ВС·СД·ВД/4S=10√10·6·2√229/(4·90)=√2290/3≈16 - это ответ.