Предмет: Математика, автор: dudnickovaira

Решите пожалйуста подробно примеры (приведенные ниже на фото)
Тема: "Вычисление неопределенного интеграла по частям"
Формула по которой решают: интеграл udv=uv- интеграл vdu

Приложения:

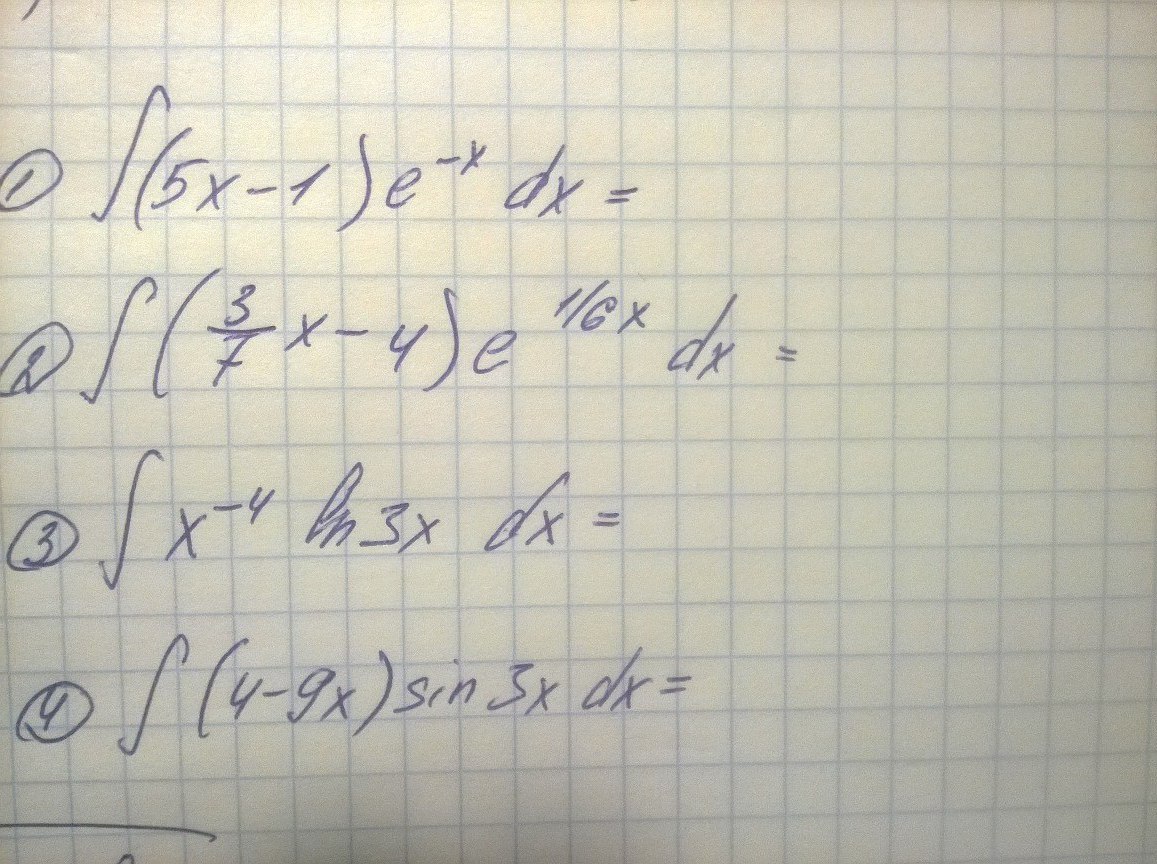
Ответы

Автор ответа: hide123

на свой страх и риск принимай решение первого. было очень давно, смутно помню. поэтому могут быть ошибки. остальные по аналогии

1) интегрирование по частям. формула есть сверху
$int {u} , dv= uv - int {v} , du$
для того чтобы решить интеграл, необходимо найти все замены и подставить их в данную формулу, с чего мы и начнем:
$int {(5x-1)( e^{-x}}) } dx =$ $[u=(5x-1) ; du = (5x-1)^{'} = 5dx,$ $dv = e^{-x}dx ; v = int {e^{-x}} dx = - e^{-x}]$
теперь подставляем в формулу:
$(5x-1)(- e^{-x})- int { -5e^{-x} } dx = (5x-1)(- e^{-x}) + 5 int { e^{-x}dx } =$ $(5x-1)(- e^{-x}) - 5 e^{-x}$

дальше приводишь подобные. еще где-то потерялась константа C наверняка, т.к. интеграл неопределенный, но не помню что с ней нужно делать.

Автор ответа: NNNLLL54

$1)int (5x-1)e^{-x}dx=[, u=5x-1,; du=5dx,; dv=e^{-x}dx,\\v=-e^{-x}; ]=-(5x-1)e^{-x}+int e^{-x}cdot 5dx=\\=-(5x-1)e^{-x}-5e^{-x}+C\\2); ; int ( frac{3}{7} x-4)e^{ frac{1}{6}x }dx=[; u= frac{3}{7} x-4; ,; du= frac{3}{7}dx,; dv=e^{frac{1}{6}x} dx,\\v=6e^{frac{1}{6}x}; ]=6( frac{3}{7}x-4)e^{frac{x}{6}} -6cdot frac{3}{7} cdot int e^{frac{x}{6}}dx=\\=6( frac{3}{7} x-4)e^{frac{x}{6}}- frac{18}{7} cdot 6cdot e^{frac{x}{6}}+C$

$3); ; int x^{-4}cdot ln3x, dx=[, u=ln3x; ,; du= frac{3}{3x} dx= frac{dx}{x} ; ,\\dv=x^{-4}dx; ,; v= frac{x^{-3}}{-3} =- frac{1}{3x^3} ; ]=- frac{ln3x}{3x^3} +int frac{dx}{3x^4} =\\=- frac{ln3x}{3x^3} +frac{1}{3}cdot frac{x^{-3}}{-3} +C\\4); ; int (4-9x)cdot ln3x; dx=[, u=ln3x,; du=frac{dx}{x}, ,\\dv=(4-9x)dx; ,; v=-frac{1}{9}cdot frac{(4-9x)^2}{2} ; ]=- frac{1}{18} (4-9x)^2cdot ln3x+$

$+frac{1}{18}cdot int frac{(4-9x)^2}{x} dx=- frac{1}{18} (4-9x)^2cdot ln3x+frac{1}{18}int frac{16-72x+81x^2}{x} dx=$

$=- frac{1}{18} (4-9x)^2cdot ln3x+ frac{1}{18} int ( frac{16}{x}-72+81x)dx=\\=- frac{1}{18} (4-9x)^2cdot ln3x+frac{1}{18}cdot (16ln|x|-72x+81cdot frac{x^2}{2} )+C$

$P.S.\\int e^{ax+b}dx=frac{1}{a}cdot e^{ax+b}+C\\int (ax+b)^{k}dx= frac{1}{a}cdot frac{(ax+b)^{k+1}}{k+1} +C$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Українська мова, автор: isolomia207

фонетичний розбір слова напрацюєшся

6 лет назад

Предмет: Математика, автор: imanalikadyrbai

Реши задачу в одном бидоне 3 л молока а в другом в четыре раза больше Сколько литров молока во втором бидоне

6 лет назад

Предмет: Физика, автор: pinksmilecp0efre

8 класс
Установите соответствие между преобразованием энергии, происходящим в техническом устройстве, и названием устройства

6 лет назад

Предмет: Обществознание, автор: tanyakan

у вас есть 500 000 куда бы вы его потратили..
это домаха по обществу
помогите написать

9 лет назад

Предмет: Биология, автор: xoxolive

Как называют независимое сокращение сердца?

9 лет назад